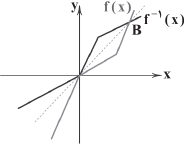
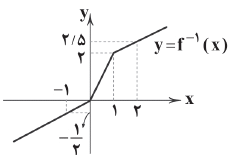
نمودار تابع $y={{f}^{-1}}(x)$ بهصورت شکل زیر است. دامنهی تابع $g(x)=\frac{1}{\sqrt{f(x)-x}}$ کدام است؟
1 )
$\left[ 0,+\infty \right)$
2 )
$\left( 0,+\infty \right)$
3 )
$\left[ 3,+\infty \right)$
$\left( 3,+\infty \right)$
پاسخ تشریحی :
تحلیل ویدئویی تست
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...