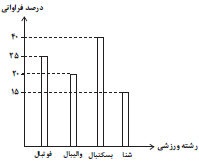
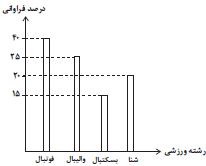
مجموع زوایای مرکزی در یک نمودار دایره‌ای برابر ${360^ \circ }$ است. با توجه به این مفهوم ابتدا زاویهٔ مرکزی مربوط به هر رشتهٔ ورزشی را می‌یابیم:

${\alpha _f} + {\alpha _v} + {\alpha _b} + {\alpha _s} = {360^ \circ }$

$\Rightarrow 6x + {15^ \circ } + 4x - {8^ \circ } + 5x - {10^ \circ } + 3x + {3^ \circ } = {360^ \circ }$

$\Rightarrow 18x = {360^ \circ } \Rightarrow x = \frac{{{{360}^ \circ }}}{{18}} = {20^ \circ }$

حال زاویهٔ مرکزی در هریک از گروه‌ها را می‌یابیم:

${\alpha _f} = 6x + {15^ \circ } = 6 \times {20^ \circ } + {15^ \circ } = {120^ \circ } + {15^ \circ } = {135^ \circ }$

${\alpha _v} = 4x + {8^ \circ } = 4 \times {20^ \circ } - {8^ \circ } = {80^ \circ } - {8^ \circ } = {72^ \circ }$

${\alpha _b} = 5x - {10^ \circ } = 5 \times {20^ \circ } - {10^ \circ } = {100^ \circ } - {10^ \circ } = {90^ \circ }$

${\alpha _s} = 3x + {3^ \circ } = 3 \times {20^ \circ } + {3^ \circ } = {60^ \circ } + {3^ \circ } = {63^ \circ }$

حال درصد مربوط به هر گروه را از تقسیم زاویهٔ مرکزی به زاویهٔ ${360^ \circ }$ ضربدر عدد 100 به‌دست می‌آوریم:

درصد فوتبال $= \frac{{{{135}^ \circ }}}{{{{360}^ \circ }}} \times 100 = 37/5\%$

درصد والیبال $= \frac{{{{72}^ \circ }}}{{{{360}^ \circ }}} \times 100 = 20\%$

درصد بسکتبال $= \frac{{{{90}^ \circ }}}{{{{360}^ \circ }}} \times 100 = 25\%$

درصد شنا $= \frac{{{{63}^ \circ }}}{{{{360}^ \circ }}} \times 100 = 17/5\%$