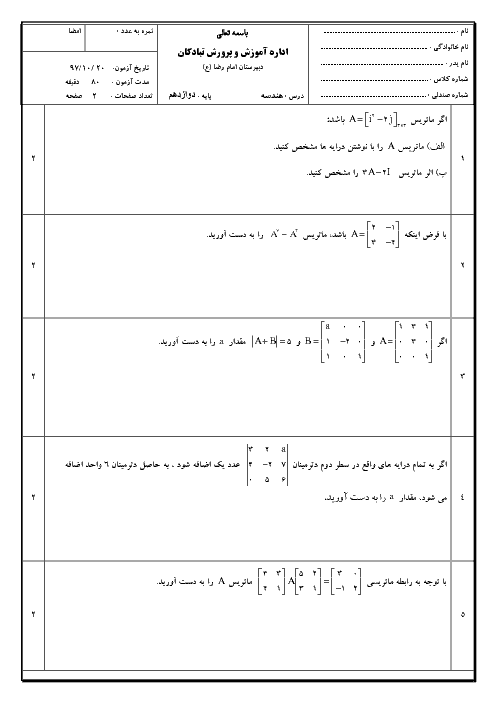
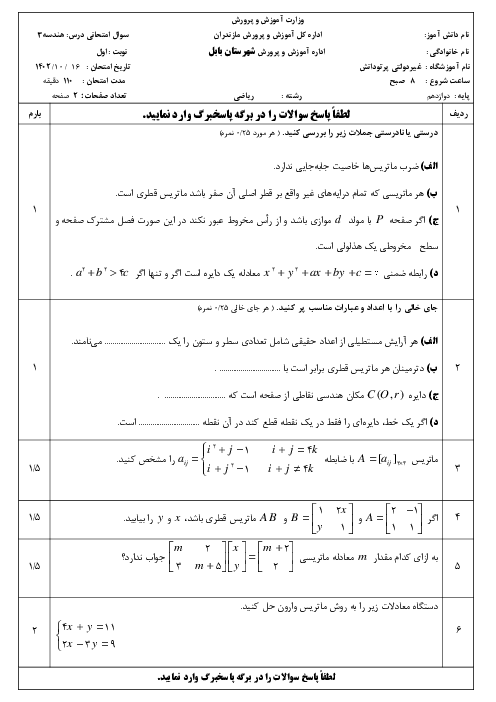
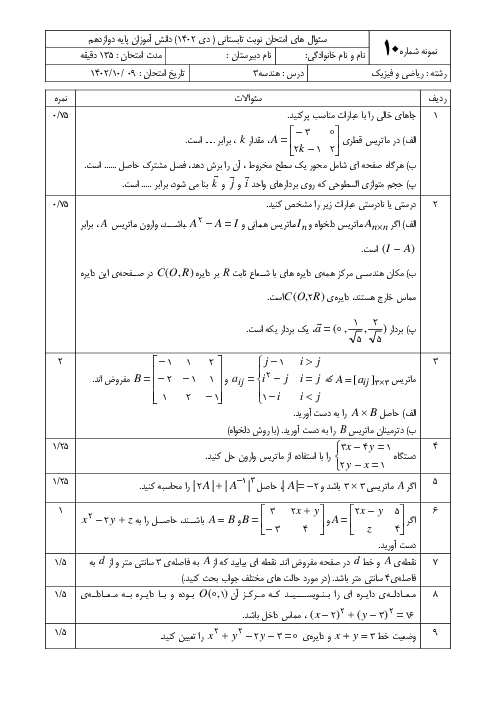
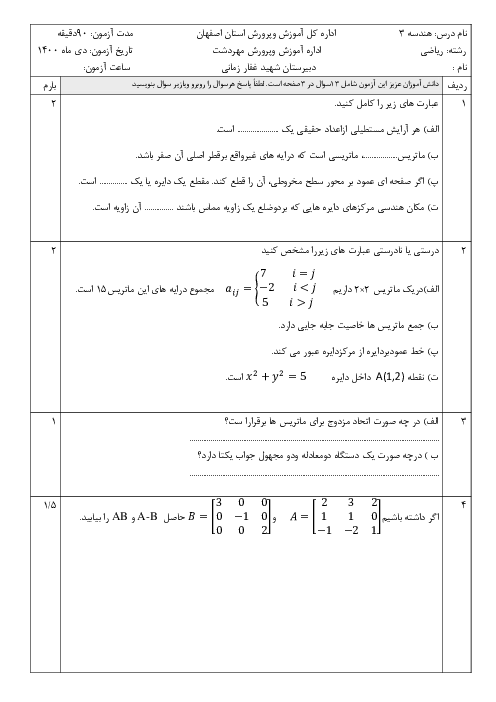
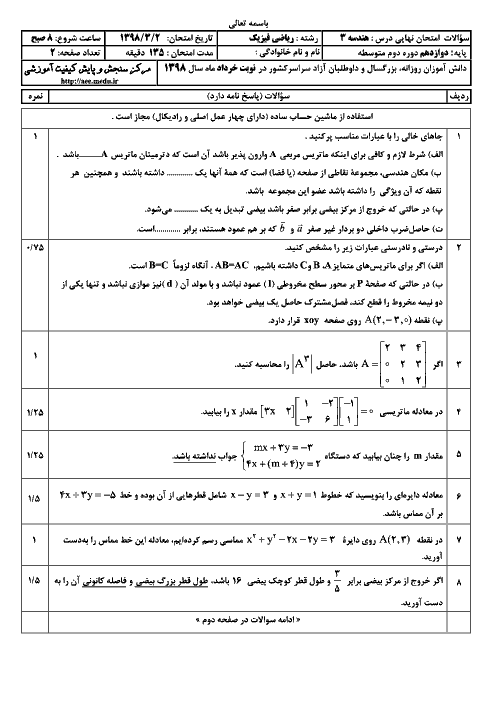
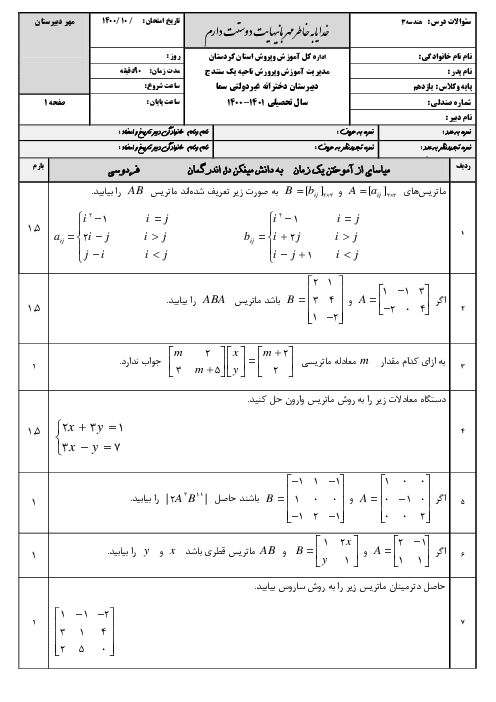
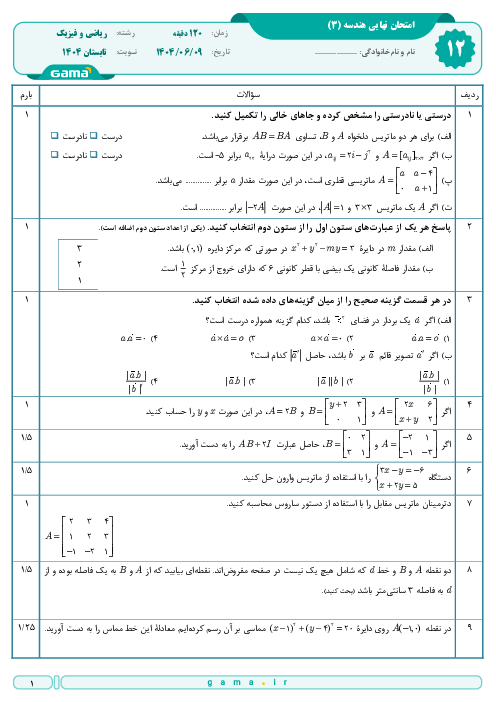
ماتریس  را معلوم کرده و ${{A}^{2}}-4A$ را به دست می‌آوریم:

$A=\left[ \begin{matrix}
   1 & 2 & 2  \\
   2 & 1 & 2  \\
   2 & 2 & 1  \\
\end{matrix} \right]\Rightarrow {{A}^{2}}-4A=\left[ \begin{matrix}
   1 & 2 & 2  \\
   2 & 1 & 2  \\
   2 & 2 & 1  \\
\end{matrix} \right]\left[ \begin{matrix}
   1 & 2 & 2  \\
   2 & 1 & 2  \\
   2 & 2 & 1  \\
\end{matrix} \right]-4\left[ \begin{matrix}
   1 & 2 & 2  \\
   2 & 1 & 2  \\
   2 & 2 & 1  \\
\end{matrix} \right]=\left[ \begin{matrix}
   9 & 8 & 8  \\
   8 & 9 & 8  \\
   8 & 8 & 9  \\
\end{matrix} \right]-\left[ \begin{matrix}
   4 & 8 & 8  \\
   8 & 4 & 8  \\
   8 & 8 & 4  \\
\end{matrix} \right]=\left[ \begin{matrix}
   5 & 0 & 0  \\
   0 & 5 & 0  \\
   0 & 0 & 5  \\
\end{matrix} \right]$

بنابراین مجموع درایه‌ها برابر $15$ است.