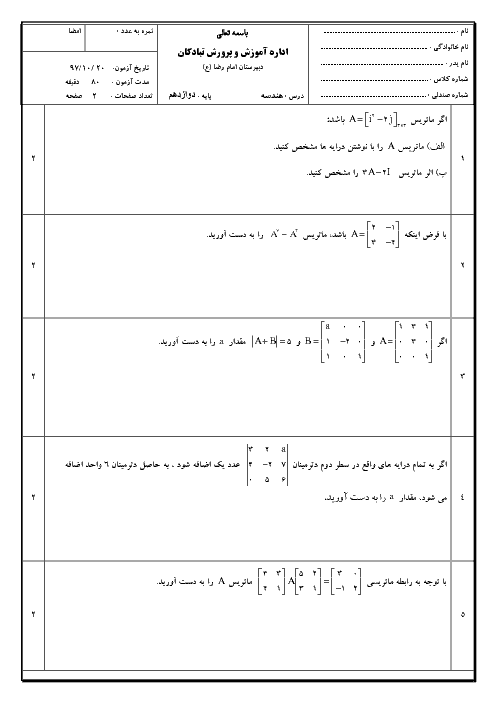
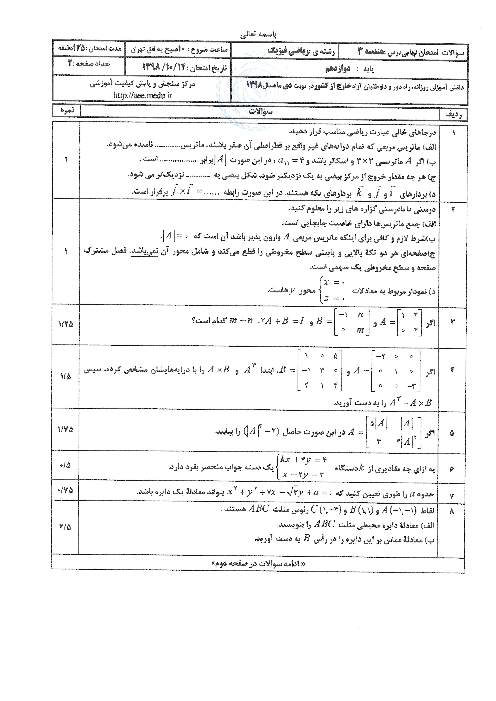
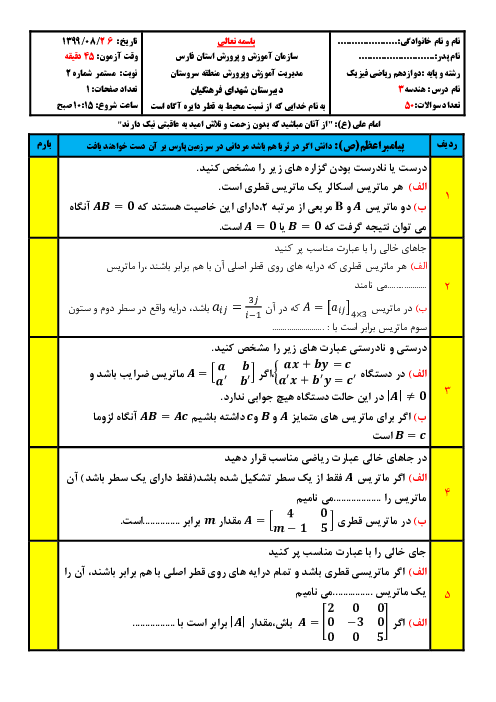
$\overrightarrow{u}=(3\overrightarrow{i}+\overrightarrow{j})\times (\overrightarrow{j}-\overrightarrow{k})=3\overrightarrow{i}\times \overrightarrow{j}-3\overrightarrow{i}\times \overrightarrow{k}+\overrightarrow{j}\times \overrightarrow{j}-\overrightarrow{j}\times \overrightarrow{k}=3\overrightarrow{k}+3\overrightarrow{j}+\overrightarrow{o}-\overrightarrow{i}=(-1,3,3)$ 

تصویر قائم $\overrightarrow{u}$ بر صفحه‌ی $xy$

${{\overrightarrow{u}}_{1}}=(-1,3,0)\Rightarrow \left| {{\overrightarrow{u}}_{1}} \right|=\sqrt{10}$

تصویر قائم $\overrightarrow{u}$ بر صفحه‌ی $yz$

\[{{\overrightarrow{u}}_{2}}=(0,3,3)\Rightarrow \left| {{\overrightarrow{u}}_{2}} \right|=3\sqrt{2}\] 

$\Rightarrow \frac{\left| {{\overrightarrow{u}}_{1}} \right|}{\left| {{\overrightarrow{u}}_{2}} \right|}=\frac{\sqrt{5}}{3}$