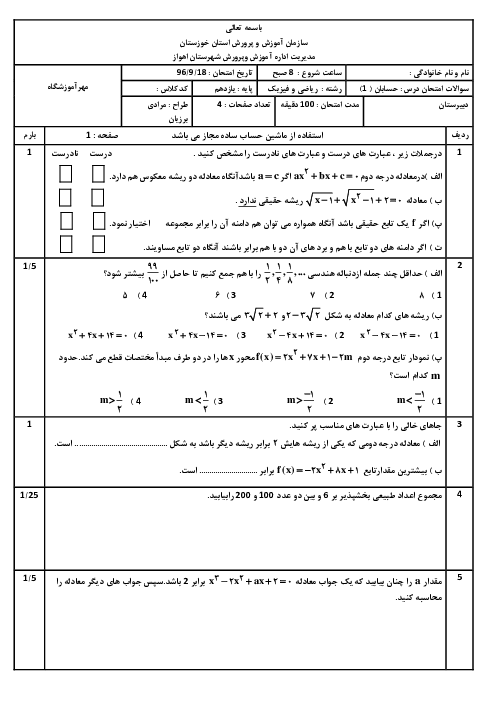
${x^2} - 3x + 1 - m = 0 \Rightarrow \alpha + \beta = 3 \Rightarrow \beta = 3 - \alpha $
$\frac{\beta }{\alpha } + \frac{\alpha }{{3 - \alpha }} = 10 \Rightarrow \frac{\beta }{\alpha } + \frac{\alpha }{\beta } = 10 \Rightarrow \frac{{{\beta ^2} + {\alpha ^2}}}{{\alpha \beta }} = 10$
$\frac{{{{(\alpha + \beta )}^2} - 2\alpha \beta }}{{\alpha \beta }} = 10 \Rightarrow \frac{{{3^2} - 2(1 - m)}}{{1 - m}} = 10 \Rightarrow \frac{{7 + 2m}}{{1 - m}} = 10$
$ \Rightarrow m = \frac{1}{4} \Rightarrow $ حالا به بررسی گزینهها میپردازیم
گزینه (3) $ - 6{x^2} - 9x - \frac{3}{4} = 0$ دارای دو ریشه منفی است. چون مجموع ریشههای آن منفی و حاصلضرب ریشههای آن مثبت است.