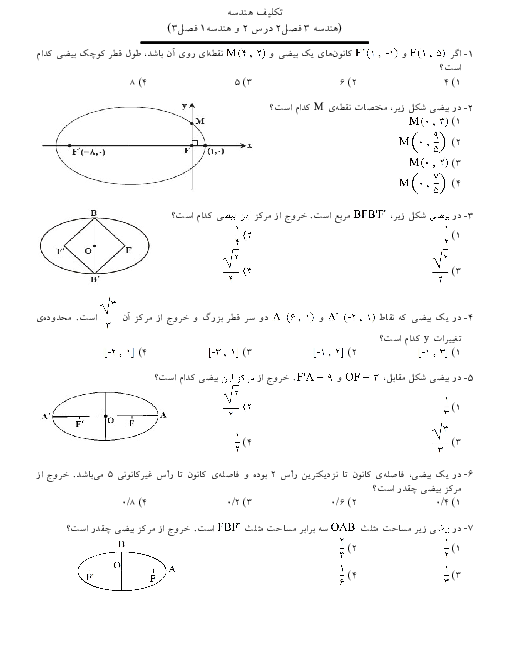
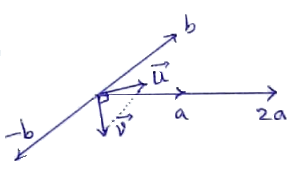
اگر $\vec u$ بردار یکه در راستای نیمساز زاویه بین بردارهای $\vec a$ و $\vec b$ و $\vec v$ بردار یکه در راستای نیمساز زاویه بین بردارهای $2\vec a$ و $ - \vec b$ باشد، مساحت مثلثی که توسط بردارهای $\vec u$ و $\vec v$ تولید می‌شود، کدام است؟
1 )
$\frac{{\sqrt 3 }}{2}$
2 )
$\frac{{\sqrt 2 }}{2}$
$\frac{1}{2}$
4 )
1
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...