درس 2: ضرب داخلی و ضرب خارجی بردارها
هندسه (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
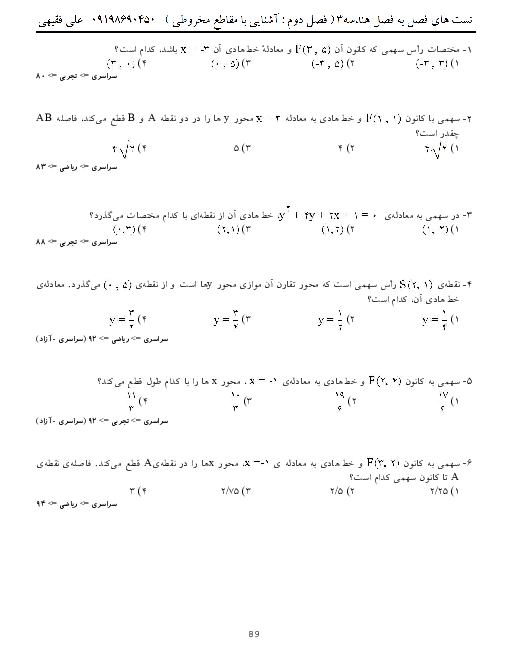
دو ماتریس $A = {\left[ {{a_{ij}}} \right]_{3 \times 3}}$ با درایه‌های به فرم ${a_{ij}} = \left\{ {\begin{array}{*{20}{c}} {1 - i}&{;\left| {i - j} \right| \leqslant 1} \\ 2&{;\left| {i - j} \right| > 1} \end{array}} \right.$ و $B = \left[ {\begin{array}{*{20}{c}} 1&{ - 1}&3 \\ 2&{ - 1}&0 \\ 3&{ - 1}&4 \end{array}} \right]$ را در نظر بگیرید.
الف) ماتریس A را به صورت آرایش مستطیلی بنویسید.
ب) حاصل $(B - I)(B + I)$ را بیابید.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...