قسمت 3: حرکت با شتاب ثابت
فیزیک (3) ریاضی
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
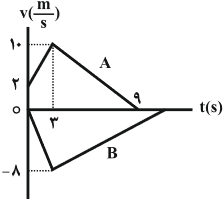
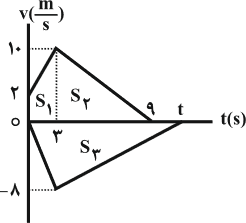
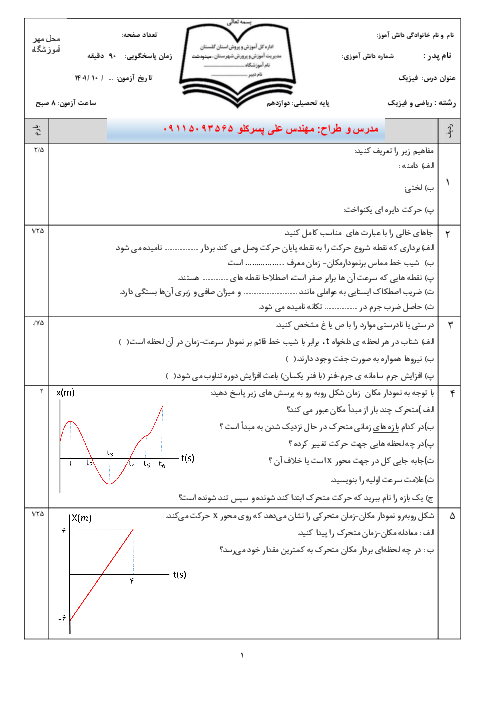
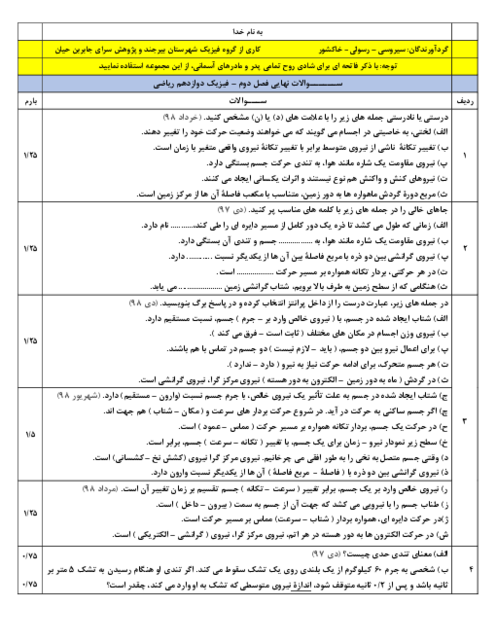
در شکل زیر، نمودار سرعت - زمان دو متحرک $A$ و $B$ که از مبدأ مکان روی محور $x$ و در دو سوی مخالف حرکت نمودهاند رسم شده است. اگر جابهجایی دو متحرک یکسان باشد، چند ثانیه پس از توقف متحرک $A$، متحرک $B$ متوقف میشود؟