جزوه و مجموعه تمرین جامع فصل اول: ماتریس و کاربردها

تعریف ماتریس و درایه‌ها

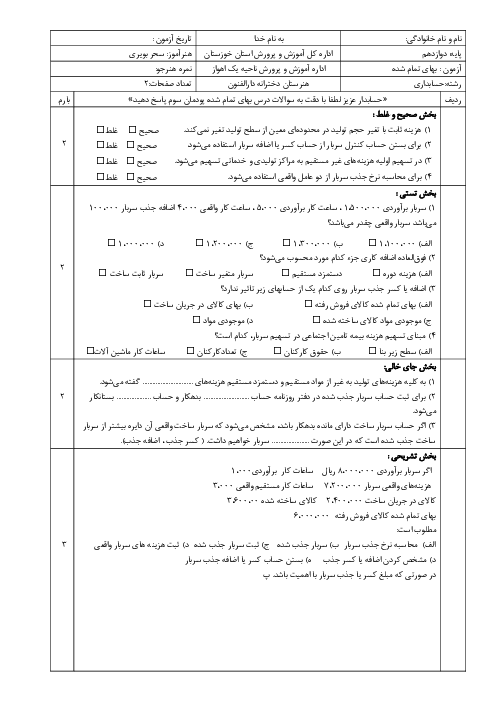
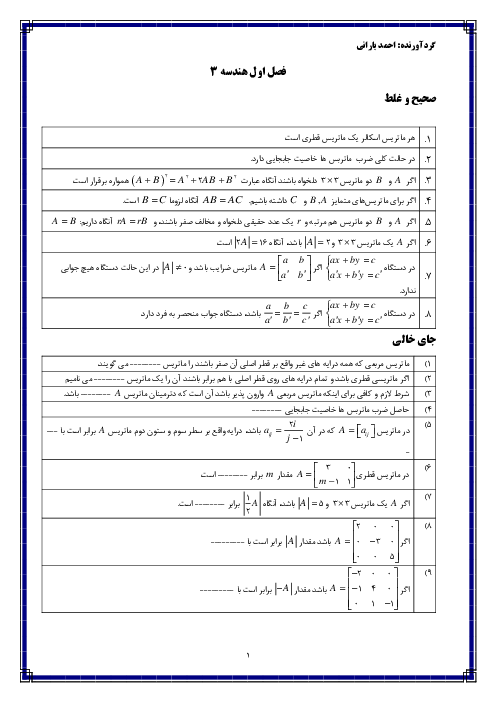
ماتریس: آرایشی مستطیلی از اعداد حقیقی که در سطرها و ستون‌ها قرار گرفته‌اند.
درایه‌های ماتریس: هر عدد حقیقی در ماتریس که در تقاطع یک سطر و یک ستون قرار دارد.
مرتبه ماتریس: تعداد سطرها و ستون‌های یک ماتریس، که به صورت "تعداد سطرها در تعداد ستون‌ها" بیان می‌شود، مانند "3 در 2".

انواع ماتریس‌ها
ماتریس مربعی: ماتریسی که تعداد سطرها و ستون‌های آن برابر است. این ماتریس‌ها دارای قطر اصلی و فرعی هستند.
ماتریس سطری: ماتریسی با تنها یک سطر.
ماتریس ستونی: ماتریسی با تنها یک ستون.
ماتریس قطری: ماتریس مربعی که در آن درایه‌های غیر از قطر اصلی صفر هستند.
ماتریس اسکالر: ماتریس قطری که درایه‌های قطر اصلی آن با هم برابرند.
ماتریس همانی (واحد): ماتریس اسکالر که درایه‌های قطر اصلی آن یک هستند.
ماتریس صفر: ماتریسی که تمام درایه‌های آن صفر است.
ماتریس بالامثلثی: ماتریس مربعی که درایه‌های زیر قطر اصلی آن صفر هستند.
ماتریس پایین‌مثلثی: ماتریس مربعی که درایه‌های بالای قطر اصلی آن صفر هستند.

جمع و تفریق ماتریس‌ها
شرط جمع‌پذیری: دو ماتریس باید هم‌مرتبه باشند تا بتوان آن‌ها را جمع یا تفریق کرد.
روش جمع و تفریق: جمع یا تفریق درایه‌های متناظر در دو ماتریس.

ضرب عدد در ماتریس
ضرب اسکالر: هر درایه ماتریس در عدد حقیقی مورد نظر ضرب می‌شود.
قرینه ماتریس: ضرب ماتریس در عدد منفی یک، که تمام درایه‌های آن را قرینه می‌کند.

دترمینان ماتریس‌ها
دترمینان ماتریس مربعی: عددی حقیقی که به هر ماتریس مربعی نسبت داده می‌شود و نشان‌دهنده ویژگی‌های خاصی از ماتریس است.
ماتریس‌های مرتبه یک: دترمینان برابر با تنها درایه ماتریس است.
ماتریس‌های مرتبه دو: دترمینان با فرمول ساده‌ای از درایه‌ها محاسبه می‌شود.
ماتریس‌های مرتبه سه: دترمینان با روش‌هایی مانند بسط سطر یا ستون و روش ساروس محاسبه می‌شود.

ویژگی‌های دترمینان
دترمینان صفر: اگر دترمینان یک ماتریس صفر باشد، ماتریس غیرمعکوس‌پذیر است.
دترمینان حاصل‌ضرب ماتریس‌ها: برابر با حاصل‌ضرب دترمینان‌های آن‌هاست.
اثر ضرایب عددی: ضرب یک عدد در ماتریس، دترمینان را به توان مرتبه ماتریس از آن عدد تغییر می‌دهد.

معکوس ماتریس
تعریف: ماتریس معکوس ماتریسی است که ضرب آن در ماتریس اصلی برابر با ماتریس همانی باشد.
شرط وجود: ماتریس باید مربعی بوده و دترمینان آن غیر صفر باشد.
روش محاسبه: از طریق تشکیل ماتریس الحاقی و تقسیم آن بر دترمینان ماتریس اصلی.

حل دستگاه معادلات خطی با استفاده از معکوس ماتریس
نمایش ماتریسی دستگاه: معادلات به صورت ماتریس ضرایب، ماتریس متغیرها و ماتریس مقادیر معلوم نوشته می‌شوند.
روش حل: اگر ماتریس ضرایب معکوس‌پذیر باشد، می‌توان با ضرب ماتریس معکوس در ماتریس مقادیر معلوم، مقادیر متغیرها را یافت.
شرایط وجود جواب:
جواب منحصر به فرد: اگر دترمینان ماتریس ضرایب غیر صفر باشد.
بی‌شمار جواب یا بدون جواب: اگر دترمینان صفر باشد و نسبت ضرایب به نسبت مقادیر معلوم تعیین‌کننده است.

این جزوه به معرفی و بررسی مفاهیم پایه‌ای ماتریس‌ها پرداخته است. با درک انواع مختلف ماتریس‌ها و عملیات‌های مرتبط مانند جمع، تفریق، ضرب و محاسبه دترمینان و معکوس ماتریس، می‌توان به حل مسائل پیچیده‌تر در ریاضیات و کاربردهای آن در علوم مختلف پرداخت. همچنین، روش حل دستگاه معادلات خطی با استفاده از معکوس ماتریس یکی از کاربردهای عملی این مباحث است که اهمیت ویژه‌ای در جبر خطی و مهندسی دارد.