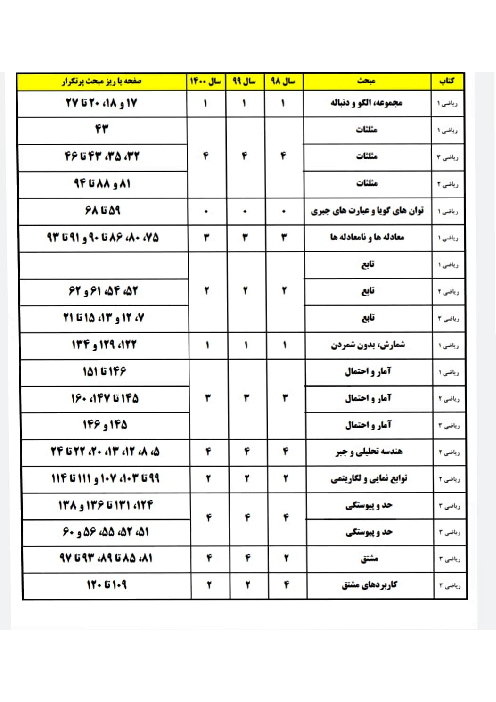
در شکل زیر، فاصلۀ نقاط A و B از خط d بهترتیب، 4 و 6 واحد است و نقطهٔ C روی خط d طوری انتخاب شده است که محیط مثلث ABC کمترین باشد. اگر مساحت چهارضلعی $ABHH'$ برابر $50\sqrt 3 $ باشد، اندازهٔ CH کدام است؟
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!