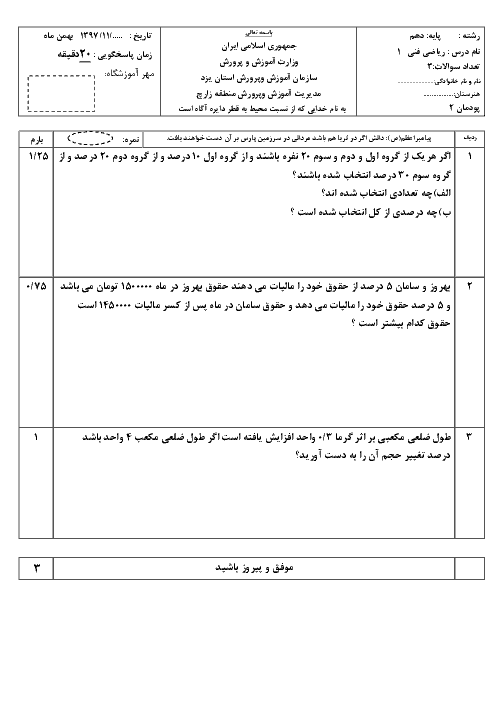
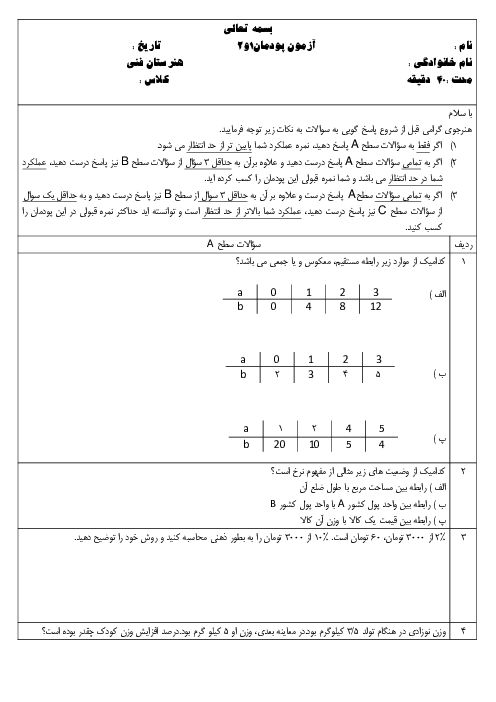
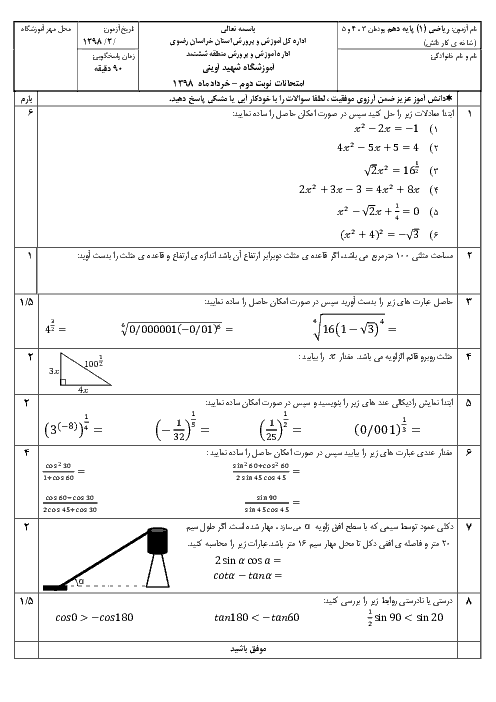
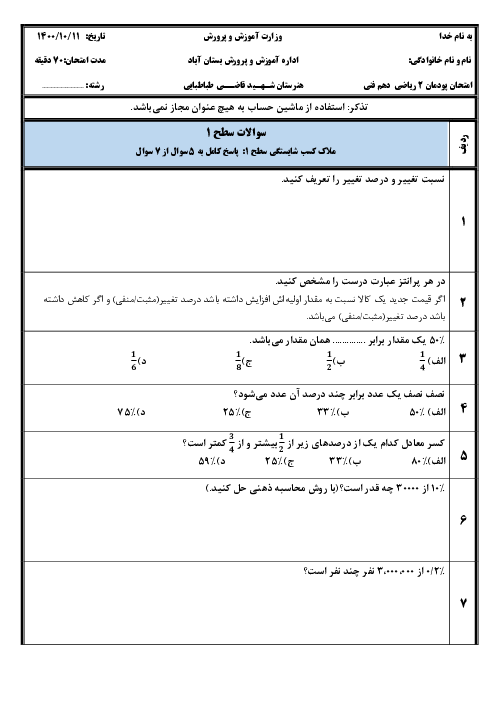
پودمان 4: توان‌رسانی به توان عددهای گویا
ریاضی1 فنی
دهم
دوره دوم متوسطه- فنی
مشترک شاخۀ فنی و حرفه‌ای
درسنامه آموزشی این مبحث
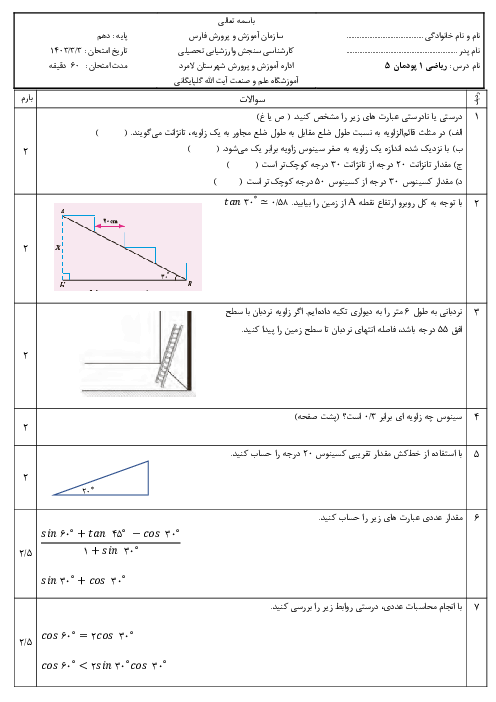
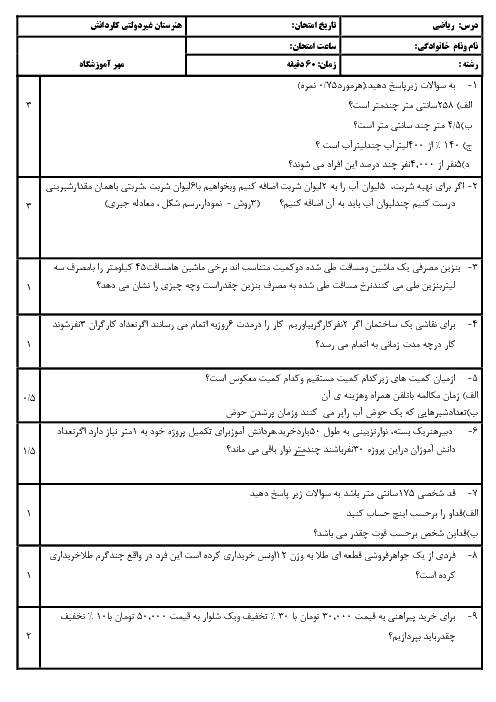
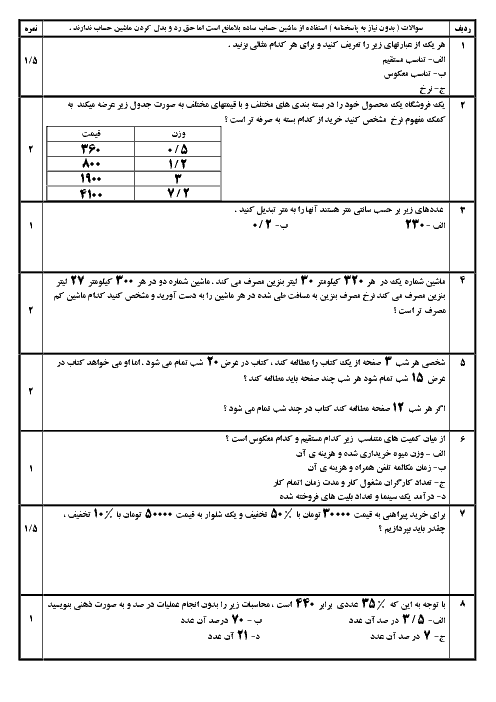
اگر $a = {27^{x + 3}}$, $b = {16^{2 - y}}$ و $\frac{a}{b} = 4$ باشد، مقدار $x + y$ کدام است؟
1 )
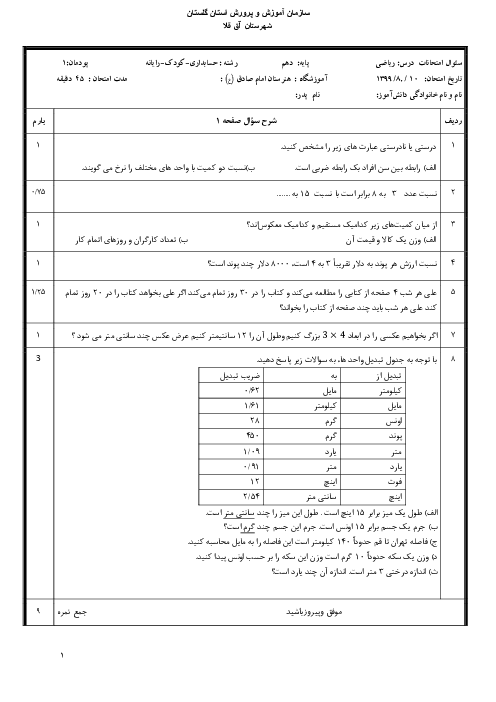
$ - \frac{{11}}{2}$
$ - \frac{1}{2}$
3 )
$\frac{1}{2}$
4 )
$\frac{{11}}{2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...