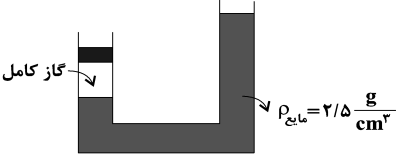
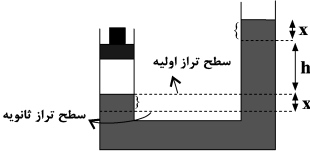
فشار گاز را در حالت اول و دوم به‌دست می‌آوریم:

$\begin{align}
  & {{P}_{1}}=\frac{mg}{A}+{{P}_{0}}\xrightarrow[A=2c{{m}^{2}}=2\times {{10}^{-4}}{{m}^{2}}]{m=2kg,g=10\frac{N}{kg},{{P}_{0}}={{10}^{5}}Pa} \\ 
 & {{P}_{1}}=\frac{2\times 10}{2\times {{10}^{-4}}}+{{10}^{5}}=2\times {{10}^{5}}Pa \\ 
 & {{P}_{2}}=\frac{{m}'g}{A}+{{P}_{0}}\xrightarrow[A=2c{{m}^{2}},{{P}_{0}}={{10}^{5}}Pa]{{m}'=2+0/5=2/5kg,g=10\frac{N}{kg}} \\ 
 & {{P}_{2}}=\frac{25}{2\times {{10}^{-4}}}+{{10}^{5}}=2/25\times {{10}^{5}}Pa \\ 
\end{align}$

اگر مایع در شاخۀ سمت چپ به اندازۀ x پایین برود در شاخۀ سمت راست به اندازۀ x بالا می‌رود، اگر فاصلۀ سطح آزاد دو مایع در حالت اول برابر با h باشد در حالت دوم برابر با h + 2x است.

$\begin{align}
  & {{P}_{1}}={{P}_{0}}+\rho gh \\ 
 & {{P}_{2}}={{P}_{0}}+\rho g(h+2x) \\ 
\end{align}$

$\begin{align}
  & \Rightarrow {{P}_{2}}-{{P}_{1}}=\rho g\times 2x\xrightarrow[g=10\frac{N}{kg},{{P}_{2}}=2/25\times {{10}^{5}}Pa,{{P}_{1}}=2\times {{10}^{5}}Pa]{\rho =2/5\frac{g}{c{{m}^{3}}}=2500\frac{kg}{{{m}^{3}}}} \\ 
 & 0/25\times {{10}^{5}}=2500\times 10\times 2x\Rightarrow x=\frac{1}{2}m=50cm \\ 
\end{align}$

نکته: می‌توان بدون محاسبۀ ${{P}_{1}}$ و ${{P}_{2}}$ سؤال را سریع‌تر حل نمود:

$\begin{align}
  & {{P}_{1}}=\frac{mg}{A}+{{P}_{0}} \\ 
 & {{P}_{2}}=\frac{{m}'g}{A}+{{P}_{0}} \\ 
 & \Rightarrow {{P}_{2}}-{{P}_{1}}=\frac{({m}'-m)g}{A}=\rho g2x \\ 
 & \Rightarrow \frac{0/5\times 10}{2\times {{10}^{-4}}}=2500\times 10\times 2\times x\Rightarrow x=\frac{1}{2}m \\ 
\end{align}$