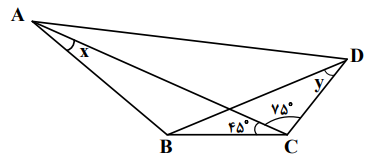
در شکل زیر، اگر $\mathop {ADB}\limits^ \wedge = \mathop {BAD}\limits^ \wedge $ و $x + y = {90^ \circ }$ باشد، مقدار $tan x$ کدام است؟
1 )
$\frac{{\sqrt 6 }}{2}$
2 )
$\frac{{\sqrt 6 }}{4}$
$\frac{{\sqrt 6 }}{3}$
4 )
$\frac{{\sqrt 6 }}{6}$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...