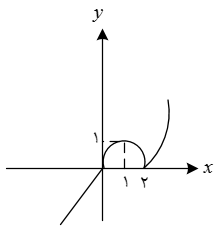
اگر نمودار تابع را رسم کنیم با ضابطه‌بندی خواهیم داشت: (شکل پایین صفحه)

$y=x\left| x-2 \right|=\left\{ \begin{matrix}
   {{x}^{2}}-2x & x\ge 2  \\
   -{{x}^{2}}+2x & x \lt 2  \\
\end{matrix} \right.$

این تابع وقتی $1 \lt x \lt 2$ نزولی است که برد آن در این فاصله $0 \lt y \lt 1$ خواهد بود. پس دامنهٔ تابع معکوس آن در این فاصله $0 \lt x \lt 1$ است که مربوط به ضابطهٔ $y=-{{x}^{2}}+2x$ می‌باشد.

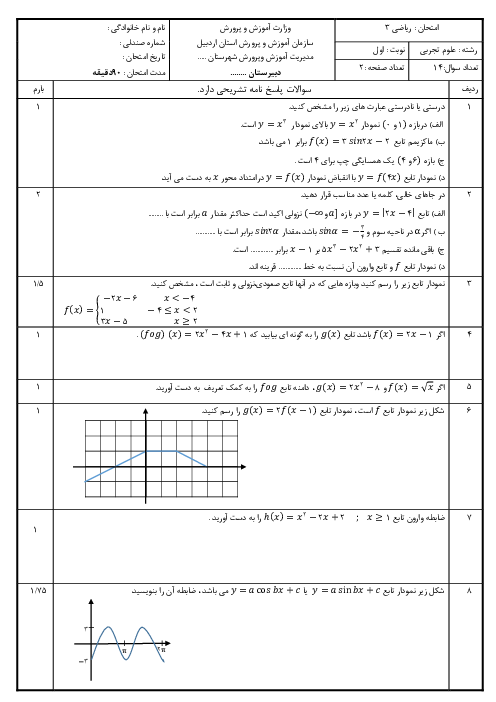
$\begin{align}
  & y=-{{x}^{2}}+2x\Rightarrow -y={{x}^{2}}-2x \\
 & \Rightarrow 1-y={{x}^{2}}-2x+1\Rightarrow {{(x-1)}^{2}}=1-y \\
 & \xrightarrow{1 \lt x \lt 2}x-1=\sqrt{1-y}\Rightarrow x=1+\sqrt{1-y} \\
 & \Rightarrow {{f}^{-1}}(x)=1+\sqrt{1-y}\,\,\,\,(0 \lt x \lt 1) \\
\end{align}$