بزرگترین بازهای را بیابید که تابع $y = {x^3} - 3x$ در آن نزولی اکید باشد.
پاسخ تشریحی :
نمایش پاسخ
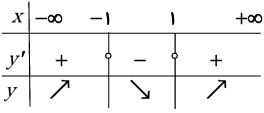
$y = {x^3} - 3x \to y' = 3{x^2} - 3 = 0 \to x = \pm 1$
با توجه به جدول تغییرات تابع، بزرگترین بازهای که تابع در آن نزولی اکید است، بازه $\left[ { - 1,1} \right]$ است.
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...