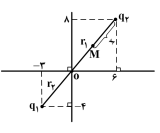
دو ذرهٔ باردار با بارهای الکتریکی ${{q}_{1}}$ و ${{q}_{2}}$، در صفحهٔ $xy$ قرار دارند. بار ${{q}_{1}}=4\mu C$ در نقطهٔ $A\left| \begin{matrix}
-3m \\
-4m \\
\end{matrix} \right.$ و بار ${{q}_{2}}=1\mu C$ در نقطهٔ $B\left| \begin{matrix}
6m \\
8m \\
\end{matrix} \right.$ قرار دارند. در چه نقطه‌ای میدان الکتریکی خالص برابر صفر است؟
1 )
$\left| \begin{matrix}
3m \\
3m \\
\end{matrix} \right.$
$\left| \begin{matrix}
3m \\
4m \\
\end{matrix} \right.$
3 )
$\left| \begin{matrix}
4m \\
3m \\
\end{matrix} \right.$
4 )
$\left| \begin{matrix}
0 \\
0 \\
\end{matrix} \right.$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...