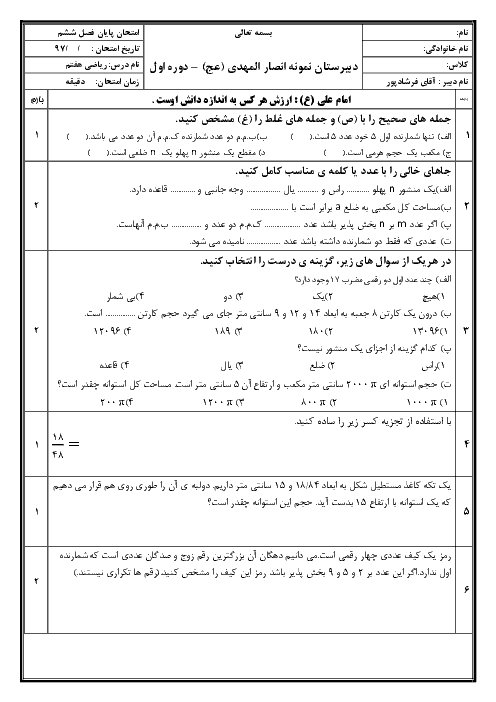
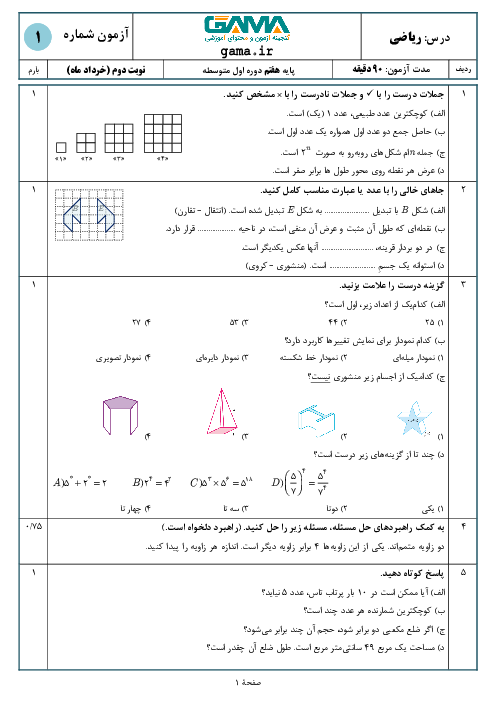
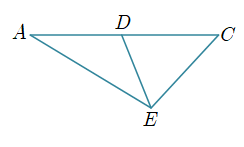
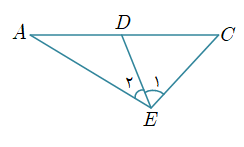
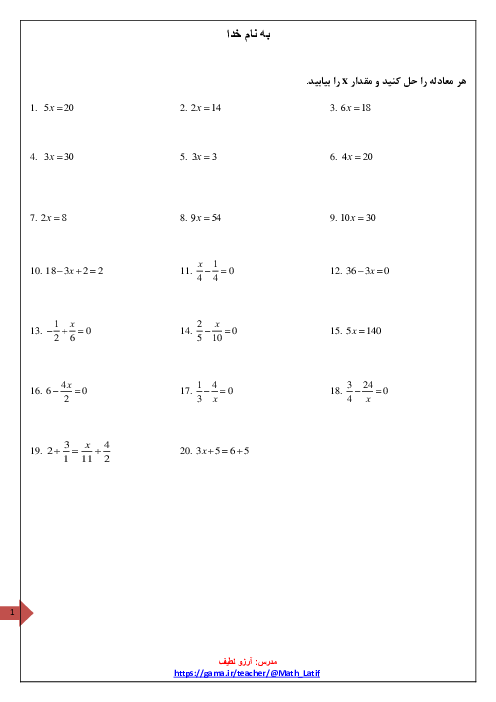در شکل زیر D وسط AC و$\overline{AD}=\overline{DE}$ میباشد. کدامیک از روابط زیر همواره صحیح است؟
1 )
$\overline{DE}=\overline{CE}$
2 )
$\overline{AE}=\overline{AC}$
3 )
$A\hat{C}E={{60}^{{}^\circ }}$
$A\hat{E}C=90{}^\circ $
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...