با توجه به نمودار f و g نمودار و ضابطه $f + g$ را بنویسید.
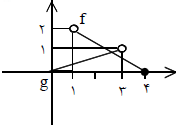
پاسخ تشریحی :
دامنهٔ $f + g$:
${D_f} = \left( {1,4} \right],{D_g} = \left[ {0,3} \right) \to {D_{f + g}} = {D_f} \cap {D_g} = \left( {1,4} \right] \cap \left[ {0,3} \right) = (1,3)$
ضابطه $f + g$:
$\eqalign{
& g:A(0,0),B(3,1) \to m = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \frac{{1 - 0}}{{3 - 0}} = \frac{1}{3} \to y - {y_1} = m(x - {x_1}) \to y = \frac{1}{3}x \cr
& \to g(x) = \frac{1}{3}x \cr
& f:C(1,2),D(4,0) \to m = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \frac{{0 - 2}}{{4 - 1}} = - \frac{2}{3} \to y - {y_1} = m(x - {x_1}) \to y - 0 = - \frac{2}{3}(x - 4) \cr
& \to f(x) = - \frac{2}{3}x + \frac{8}{3} \cr
& (f + g)(x) = f(x) + g(x) = \frac{1}{3}x - \frac{2}{3}x + \frac{8}{3} = - \frac{1}{3}x + \frac{8}{3} \cr} $
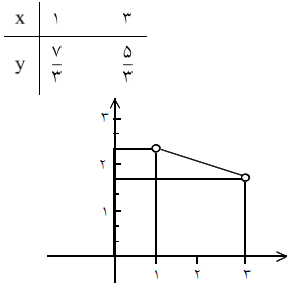
نمودار $f + g$: (شکل)
$(f + g)(x) = - \frac{1}{3}x + \frac{8}{3}$
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!