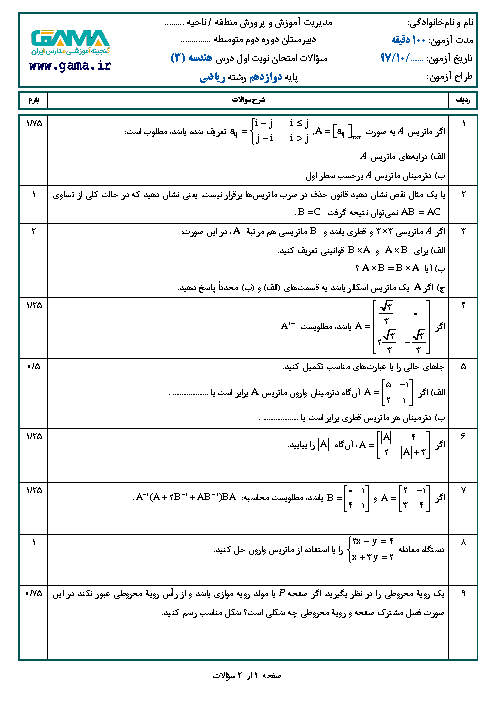
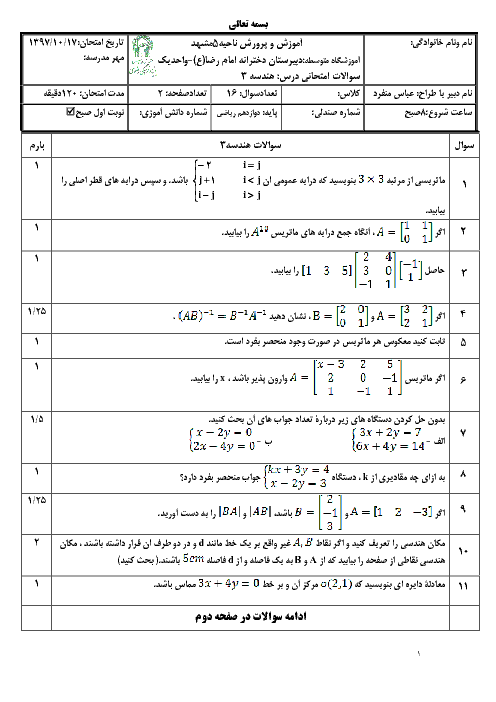
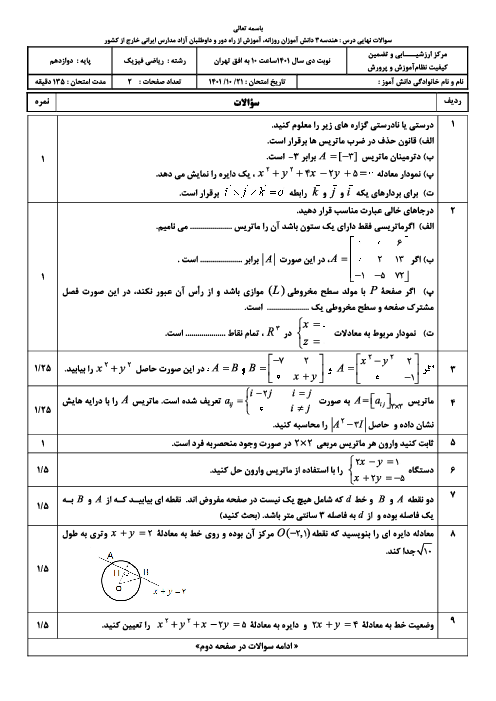
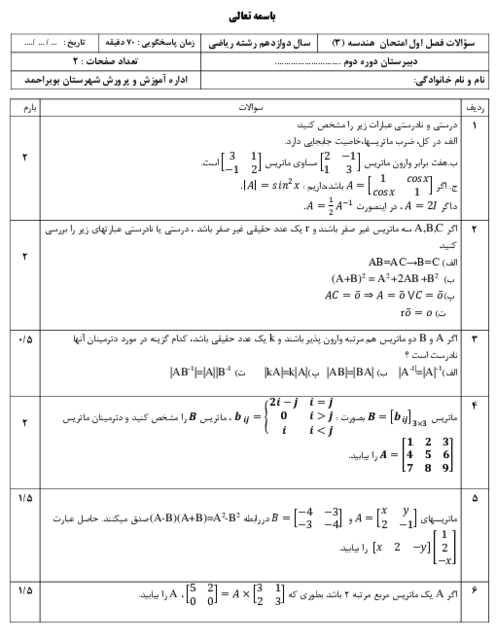
نکته: اگر $A$ ماتریسی مربعی باشد، توان‌های $A$ را به‌صورت ${{A}^{2}}=A\times A$، ${{A}^{3}}={{A}^{2}}\times A$، ... و ${{A}^{n}}={{A}^{n-1}}\times A$ تعریف می‌کنیم.

نکته: اگر ماتریس‌های $A$ و $B$ تعویض‌پذیر باشند $(AB=BA)$، آنگاه همۀ اتحادهای جبری برای آن‌ها برقرار است.

نکته: ماتریس همانی $I$ با هر ماتریسی تعویض‌پذیر است. $(AI=IA)$ 

ابتدا ماتریس ${{A}^{2}}$ را به‌دست می‌آوریم:

${{A}^{2}}=\left[ \begin{matrix} \begin{matrix} {{\operatorname{Cos}}^{2}}\alpha  & \operatorname{Sin}\alpha \operatorname{Cos}\alpha \\ \end{matrix}  \\ \begin{matrix} \operatorname{Sin}\alpha \operatorname{Cos}\alpha  & {{\operatorname{Sin}}^{2}}\alpha \\ \end{matrix}  \\ \end{matrix} \right]\left[ \begin{matrix} \begin{matrix} {{\operatorname{Cos}}^{2}}\alpha  & \operatorname{Sin}\alpha \operatorname{Cos}\alpha \\ \end{matrix}  \\ \begin{matrix} \operatorname{Sin}\alpha \operatorname{Cos}\alpha  & {{\operatorname{Sin}}^{2}}\alpha \\ \end{matrix}  \\ \end{matrix} \right]$

$=\left[ \begin{matrix} \begin{matrix} {{\operatorname{Cos}}^{4}}\alpha +{{\operatorname{Sin}}^{2}}\alpha {{\operatorname{Cos}} ^{2}}\alpha  & \operatorname{Sin}\alpha {{\operatorname{Cos}}^{3}}\alpha +{{\operatorname{Sin}}^{3}}\alpha \operatorname{Cos}\alpha   \\ \end{matrix}  \\ \begin{matrix} \operatorname{Sin}\alpha {{\operatorname{Cos}}^{3}}\alpha +{{\operatorname{Sin}}^ {3}}\alpha \operatorname{Cos}\alpha  & {{\operatorname{Sin}}^{2}}\alpha {{\operatorname {Cos}}^{2}}\alpha +{{\operatorname{Sin}}^{4}}\alpha   \\ \end{matrix}  \\ \end{matrix} \right]$

$=\left[ \begin{matrix} \begin{matrix} {{\operatorname{Cos}}^{2}}\alpha ({{\operatorname{Cos}}^{2}}\alpha +{{\operatorname {Sin}}^{2}}\alpha ) & \operatorname{Sin}\alpha \operatorname{Cos}\alpha ({{\operatorname {Cos}}^{2}}\alpha +{{\operatorname{Sin}}^{2}}\alpha )  \\ \end{matrix}  \\ \begin{matrix} \operatorname{Sin}\alpha \operatorname{Cos}\alpha ({{\operatorname{Cos}}^{2}}\alpha +{{\operatorname{Sin}}^{2}}\alpha ) & {{\operatorname{Sin}}^{2}}\alpha ({{\operatorname {Cos}}^{2}}\alpha +{{\operatorname{Sin}}^{2}}\alpha )  \\ \end{matrix}  \\ \end{matrix} \right]$

$=\left[ \begin{matrix} \begin{matrix} {{\operatorname{Cos}}^{2}}\alpha   \\ \operatorname{Sin}\alpha \operatorname{Cos}\alpha   \\ \end{matrix} & \begin{matrix} \operatorname{Sin}\alpha \operatorname{Cos}\alpha   \\ {{\operatorname{Sin}}^{2}}\alpha   \\ \end{matrix}  \\ \end{matrix} \right]=A$

بنابراین ${{A}^{2}}=A$. اکنون داریم:

${{(I-A)}^{2}}={{I}^{2}}+{{A}^{2}}-2A=I+A-2A=I-A\Rightarrow {{(I-A)}^{3}}={{(I-A)}^{2}}=I-A\Rightarrow {{(I-A)}^{4}}={{(I-A)}^{3}}=I-A\Rightarrow ....\Rightarrow {{(I-A)}^{100}}=I-A$