نمودار تابع و يكديگر را در نقاط به طول‌های 2 و 2- قطع می‌كنند، مقدار كدام است؟ | ریاضی و آمار (2) یازدهم شماره 50849

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

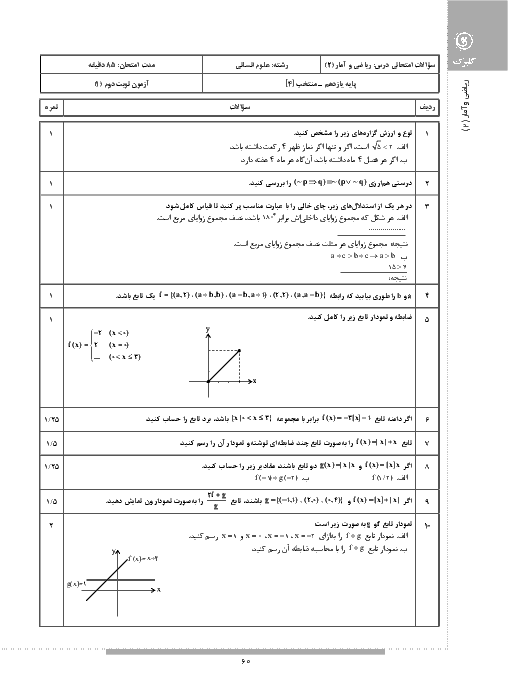
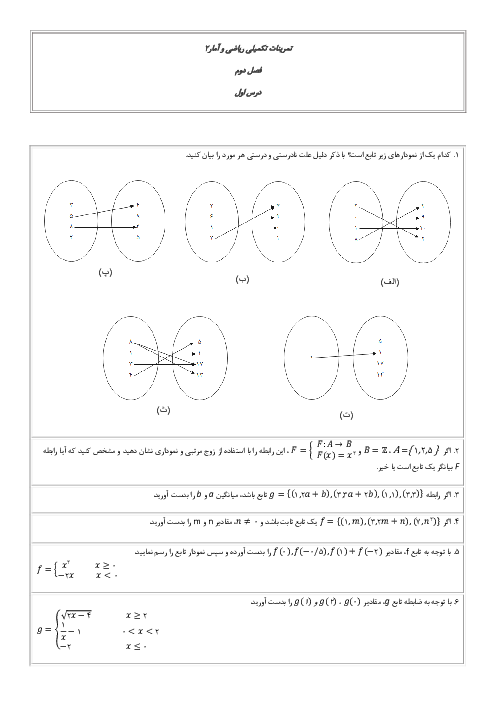
درس 2: توابع پلکانی و قدر مطلقی ریاضی و آمار (2) یازدهم متوسطه دوم نظری ادبیات و علوم انسانی درسنامه آموزشی این مبحث

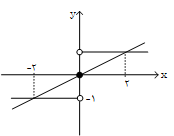
نمودار تابع $f(x)=sign(x)$ و $g(x)=ax$ يكديگر را در نقاط به طول‌های 2 و 2- قطع می‌كنند، مقدار $a$ كدام است؟

1 )

2 )

3 )

$\frac{1}{2}$

4 )

$-\frac{1}{2}$

نمایش پاسخ

ابتدا نمودار دو تابع را در يک دستگاه مختصات رسم می‌كنيم، دقت كنيد با توجه به نمودار تابع علامت درمی‌یابيم كه چون تابع $g(x)$ تابع $f(x)$ را در دو نقطه به طول‌های $-2,2$ قطع كرده است، لذا می‌بايست $a \gt 0$ باشد و نمودار آن به صورت زير در شكل رسم شده است.

$f(x)=sign(x)=\left\{ \begin{matrix} 1,x\gt 0 \\ 0,x=0 \\ -1,x\lt 0 \\ \end{matrix} \right.$

با توجه به نمودار تابع $g(x)$ به‌ازای $x=2$ مقدار تابع $g(2)=1$ و به‌ازای $x=-2$ مقدار تابع $g(-2)=-1$ است، حال داریم:

$g(2)=1\Rightarrow g(2)=2a=1\Rightarrow a=\frac{1}{2}$