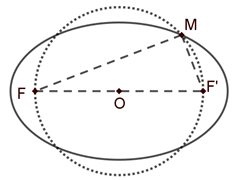
یک بیضی با قطر بزرگ و کوچک 2a و 2b مفروض است. دایرهای هممرکز با بیضی از کانونهای بیضی عبور میکند و بیضی را در 4 نقطه قطع میکند، یکی از نقاط برخورد را M مینامیم. ثابت کنید:
الف) مثلث $MFF'$ قائمالزاویه است.
ب) مساحت مثلث $MFF'$ برابر با ${b^2}$ است.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!