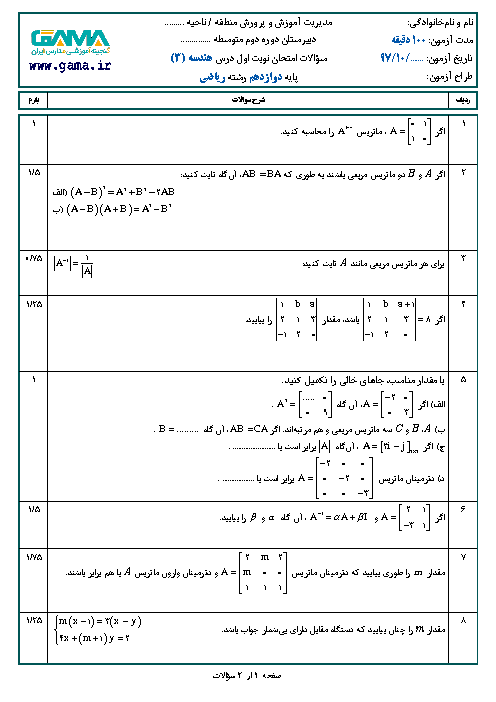
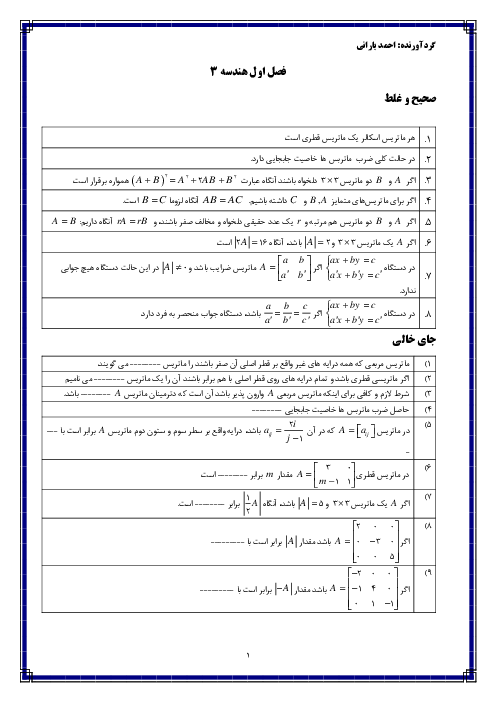
درس 2: ضرب داخلی و ضرب خارجی بردارها
هندسه (3)
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
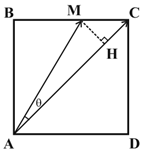
چند نقطه مانند $M$ روی محيط مربع $ABCD$ وجود دارد كه $\overrightarrow{AM}.\overrightarrow{AC}=\frac{1}{2}{{\left| \overrightarrow{AC} \right|}^{2}}$ باشد؟