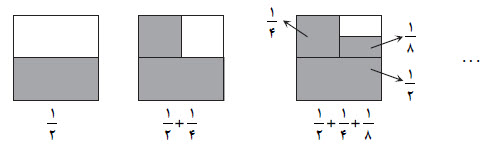
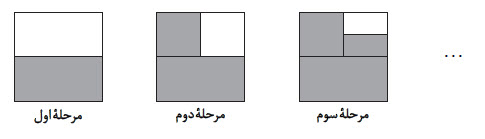
مربعی به ضلع ۱ واحد مفروض است. در مرحلۀ اول آن را به دو مستطيل مساوی تقسيم میكنيم و يكی از آنها را رنگ میكنيم. در مرحلۀ دوم مستطيل رنگ نشده را به دو مربع مساوی تقسيم كرده و يكی از آنها را رنگ میكنيم. اگر اين كار را ادامه دهيم، در مرحلۀ هفتم، مساحت قسمت رنگشده كدام است؟
1 )
$\frac{31}{32}$
2 )
$\frac{63}{64}$
$\frac{127}{128}$
4 )
$\frac{255}{256}$
پاسخ تشریحی :