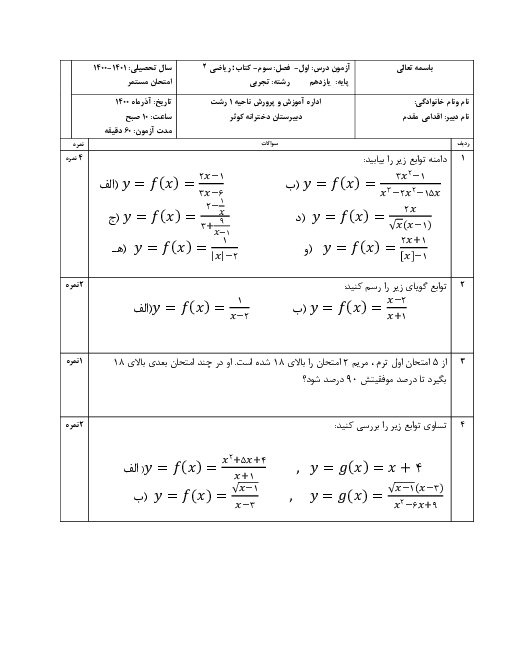
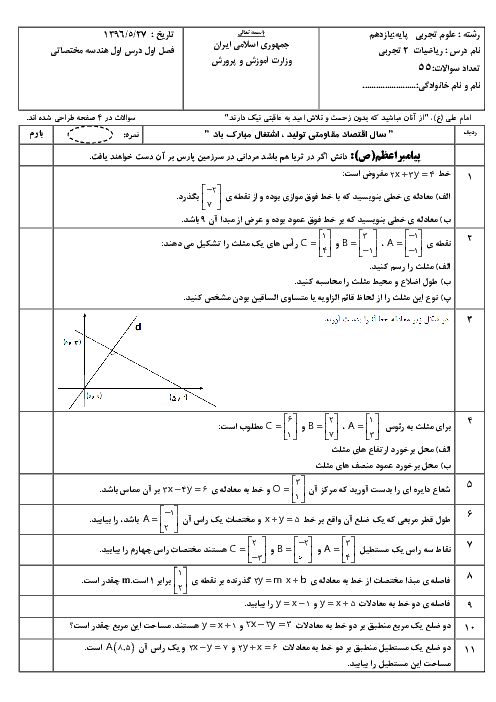
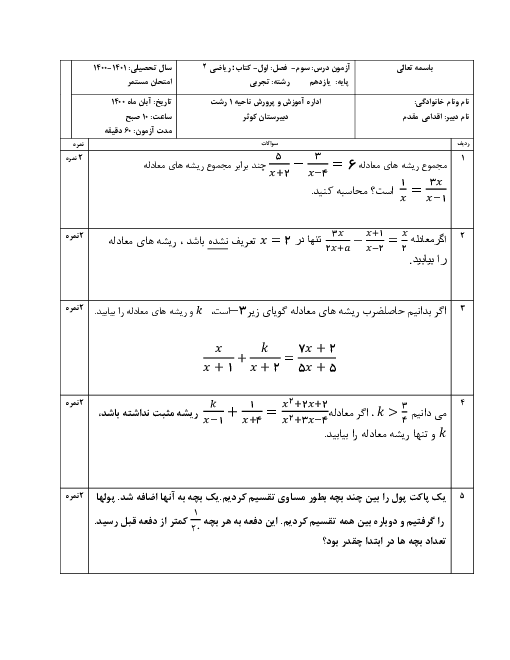
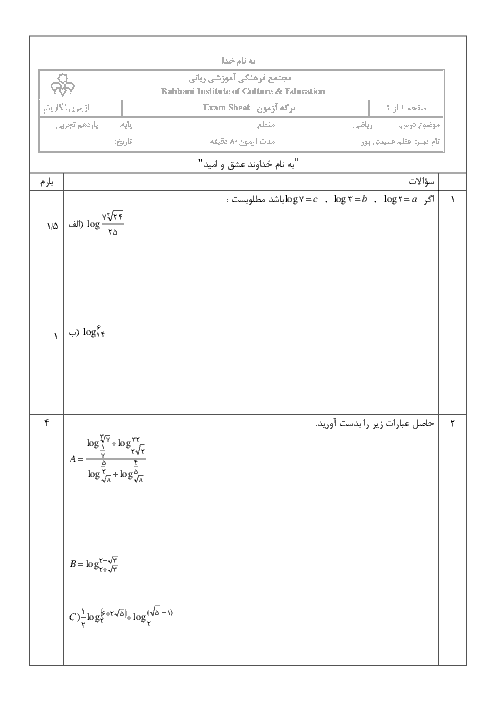
درس 2: معادلهٔ درجهٔ دوم و تابع درجه 2
ریاضی (2)
یازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
به ازای کدام مقدار k ریشههای معادلهٔ $4{{x}^{2}}+kx-5=0$ معکوس ریشههای معادلهٔ $x(5x+3)=4$ است؟