درس 1: مفاهیم اولیه و زاویه‌ها در دایره
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
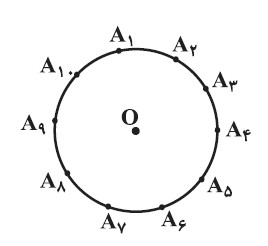
در دایرۀ زیر، نقاط ${{A}_{1}},{{A}_{2}},...,{{A}_{10}}$ به فاصله‌های مساوی از یکدیگر قرار گرفته‌اند. اگر نقطه O مرکز دایره باشد، زاویۀ ${{A}_{1}}{{\hat{A}}_{5}}O$ برابر با کدام گزینه است؟
1 )
${{36}^{{}^\circ }}$
2 )
${{10}^{{}^\circ }}$
${{18}^{{}^\circ }}$
4 )
${{72}^{{}^\circ }}$
پاسخ تشریحی :
تحلیل ویدئویی تست
مرضیه موثقی 
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...