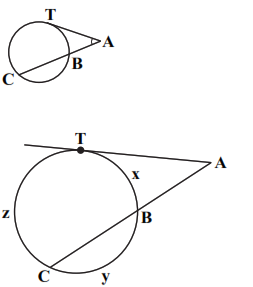
درس 1: مفاهیم اولیه و زاویهها در دایره
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
در شکل زیر اگر $\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$، اندازهی زاویهی A کدام است؟
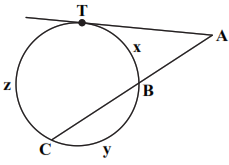
1 )
${{36}^{{}^\circ }}$
${{54}^{{}^\circ }}$
3 )
${{72}^{{}^\circ }}$
4 )
${{48}^{{}^\circ }}$
پاسخ تشریحی :