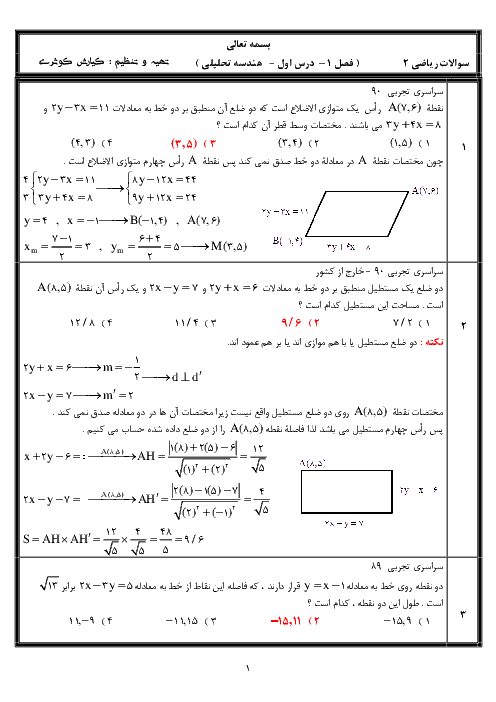
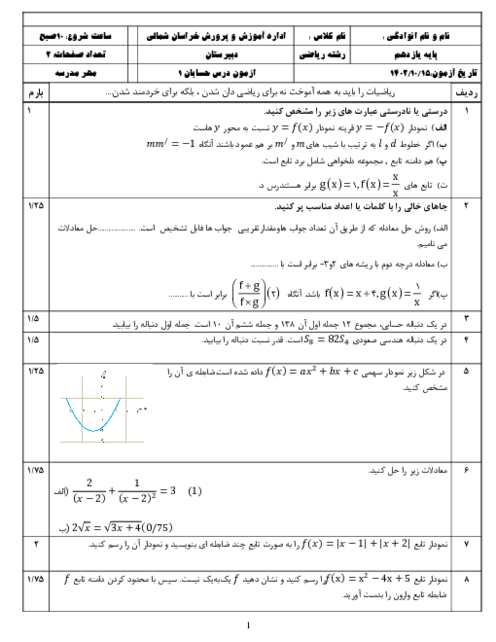
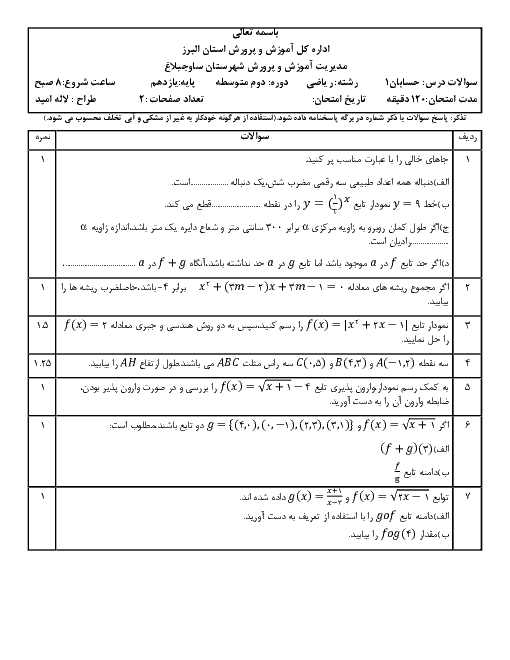
به ازای چه مقداری از m هر دو ریشهٔ معادلهٔ عبارت درجه دوم در بازهٔ قرار می‌گیرد؟ | حسابان (1) یازدهم شماره 379048 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت اول آزمون ماهانه نمونه سوال گام به گام طرح درس کاربرگ تیزهوشان هنرستان تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم‌ها

فصل 1: جبر و معادله حسابان (1) یازدهم متوسطه دوم نظری علوم ریاضی درسنامه آموزشی این مبحث

به ازای چه مقداری از m هر دو ریشهٔ معادلهٔ عبارت درجه دوم ${x^2} - mx + m - 3 = 0$ در بازهٔ $(0,1)$ قرار می‌گیرد؟

نمایش پاسخ

شرایط اینکه دو ریشه در بازه $(0,1)$ قرار گیرند برابر به صورت $\Delta > 0,S > 0,0 < P < 1$ است.

$\eqalign{
& \Delta = {m^2} - 4m + 12 > 0 \cr
& S = m > 0 \to m \in (0, + \infty ) \cr
& P = m - 3 \to 0 < m - 3 < 1 \to 3 < m < 4 \cr} $

با اشتراک گرفتن از هر سه مورد به دست آمده مقدار $3 < m < 4$ به دست می‌آید.

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

منتظریم اولین نفر تحلیلش کنه!

ویدیو دوره آموزشی، حسابان (1) یازدهم متوسطه دوم نظری

مدرس: عادل نوری

مدت دوره: 4 ساعت (7 فایل)

با گنجینه سوال، آزمون دلخواهتو بساز

سوپراستار

بسته ویژه نمره بیست: 5 نمونه سوال شبه نهایی حسابان (1) یازدهم ریاضی

21 صفحه

بسته ویژه نمره بیست: 5 نمونه سوال شبه نهایی حسابان (1) یازدهم ریاضی

ويژه نامه نوبت اول و…

رایـــــگان

آزمون آمادگی امتحان نوبت اول حسابان (1) پایه یازدهم ریاضی | دبیرستان سرای دانش واحد حافظ

4 صفحه

آزمون آمادگی امتحان نوبت اول حسابان (1) پایه یازدهم ریاضی | دبیرستان سرای…

کلاس یازدهمی

سوالات تستی حسابان (1) یازدهم | آشنایی با هندسه تحلیلی

17 صفحه

سوالات تستی حسابان (1) یازدهم | آشنایی با هندسه تحلیلی

کیارش کوثری

سوالات آزمون نوبت دوم حسابان (1) یازدهم دبیرستان پیروان امام علی تهران | خرداد 1400

9 صفحه

سوالات آزمون نوبت دوم حسابان (1) یازدهم دبیرستان پیروان امام علی تهران…

داوود شهریاری

رایـــــگان

نمونه سوالات امتحانی حسابان (1) پایه یازدهم رشته ریاضی با پاسخ | فصل اول- درس 1: مجموع جملات دنباله‌های حسابی و هندسی

7 صفحه

نمونه سوالات امتحانی حسابان (1) پایه یازدهم رشته ریاضی با پاسخ | فصل اول-…

کلاس یازدهمی

جزوه آموزشی دست نویس حسابان (1) یازدهم | فصل 4: مثلثات

34 صفحه

جزوه آموزشی دست نویس حسابان (1) یازدهم | فصل 4: مثلثات

بیتا سلیمانی امیری

سوالات تستی حسابان (1) یازدهم رشته رياضی | فصل اول (درس 1 و 2)

4 صفحه

سوالات تستی حسابان (1) یازدهم رشته رياضی | فصل اول (درس 1 و 2)

آرمین حیدری

نمونه سوال آزمون نوبت اول حسابان 1 دبیرستان نجابت دی 1402

5 صفحه

نمونه سوال آزمون نوبت اول حسابان 1 دبیرستان نجابت دی 1402

سمیه قربانی

رایـــــگان

118 سوال تستی حسابان (1) پایه یازدهم رشته ریاضی | فصل اول- درس 4: قدر مطلق و ویژگی های آن

19 صفحه

118 سوال تستی حسابان (1) پایه یازدهم رشته ریاضی | فصل اول- درس 4: قدر…

کلاس یازدهمی

آزمون نوبت دوم حسابان (1) یازدهم دبیرستان البرز هشتگرد | اردیبهشت 1397

2 صفحه

آزمون نوبت دوم حسابان (1) یازدهم دبیرستان البرز هشتگرد | اردیبهشت 1397

حامد فرشاد

احساسات خوشایند و ناخوشایند: احساساتی که تأثیر مثبت یا منفی بر فرد دارند.

کپسول آموزشی

احساسات خوشایند و ناخوشایند: احساساتی که تأثیر مثبت یا منفی بر فرد دارند.
1404/08/6

اثبات با همنهشتی: استفاده از برابری اجزای متناظر برای اثبات

کپسول آموزشی

اثبات با همنهشتی: استفاده از برابری اجزای متناظر برای اثبات
1404/09/10

خلاصه کتاب همسایه ها نوشته احمد محمود

خلاصه کتاب

خلاصه کتاب همسایه ها نوشته احمد محمود
1404/05/7

گزارش علمی: نوشتن نتایج آزمایش و استنتاج‌ها به‌صورت منظم و دقیق

کپسول آموزشی

گزارش علمی: نوشتن نتایج آزمایش و استنتاج‌ها به‌صورت منظم و دقیق
1404/08/27

میعان: تبدیل گاز به مایع

کپسول آموزشی

میعان: تبدیل گاز به مایع
1404/09/12

شخصیت کاریزماتیک: فردی که به دلیل ویژگی‌های فردی یا جایگاه اجتماعی نفوذ بالایی بر مخاطبان دارد.

کپسول آموزشی

شخصیت کاریزماتیک: فردی که به دلیل ویژگی‌های فردی یا جایگاه اجتماعی نفوذ…
1404/10/17

نیروی تماسی و غیرتماسی چیست؟

کپسول آموزشی

نیروی تماسی و غیرتماسی چیست؟
1404/07/5

مدرسه‌های قدیمی، حافظه زنده تاریخ علم و ادب در کهن دیار تبریز

اخبار آموزش و پرورش

مدرسه‌های قدیمی، حافظه زنده تاریخ علم و ادب در کهن دیار تبریز

نقش‌های خانوادگی: وظایف و جایگاه‌هایی که رسانه برای پدر، مادر و فرزندان تصویر می‌کند.

کپسول آموزشی

نقش‌های خانوادگی: وظایف و جایگاه‌هایی که رسانه برای پدر، مادر و فرزندان…
1404/10/16

دیافراگم؛ ماهیقه جداکننده قفسه سینه از شکم، نقش کلیدی در دم و بازدم

کپسول آموزشی

دیافراگم؛ ماهیقه جداکننده قفسه سینه از شکم، نقش کلیدی در دم و بازدم
1404/06/29

موارد بیشتر

موارد بیشتر

ارسال فایل

حل مسائل حسابان یازدهم

مقدار c کدام است؟

در یک دنباله حسابی داریم sn:4n²-n. جمله هفتم را بیابید.

موارد بیشتر

ارسال پرسش

موارد بیشتر