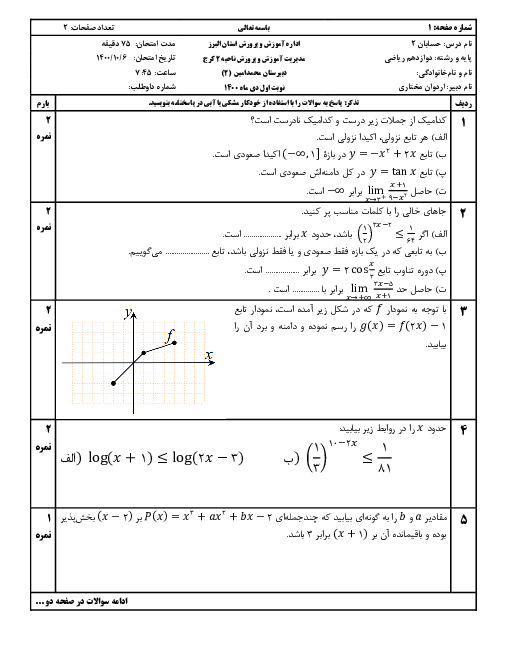
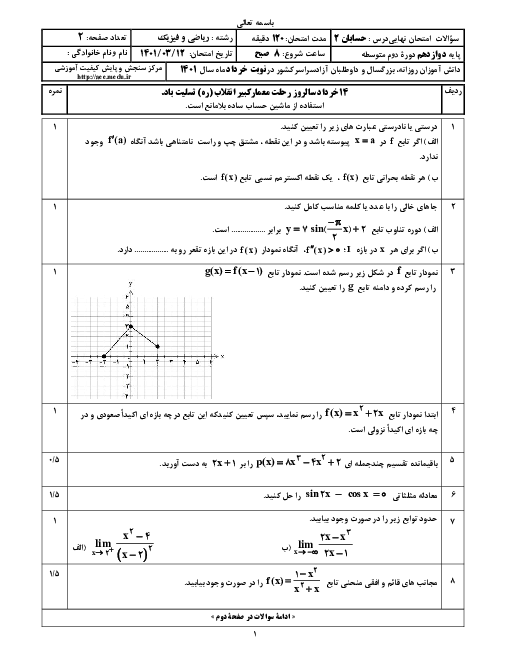
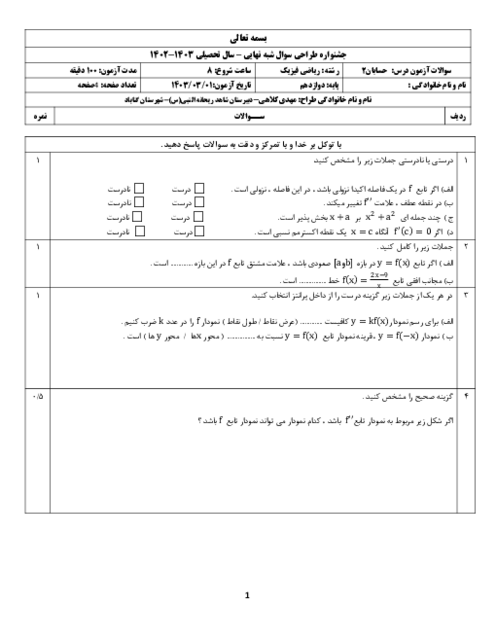
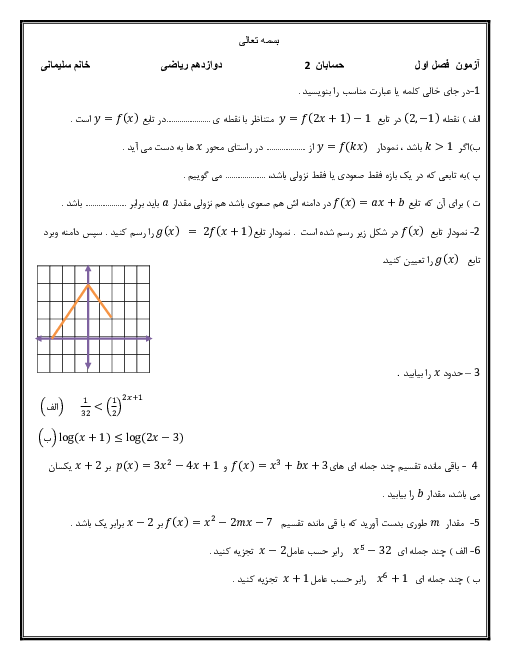
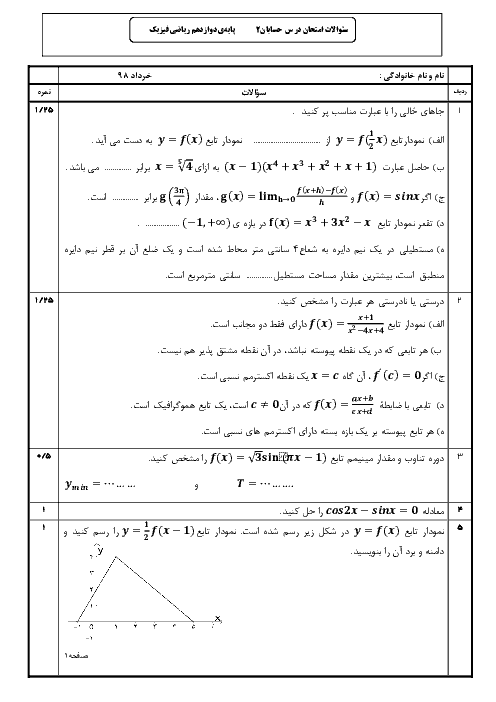
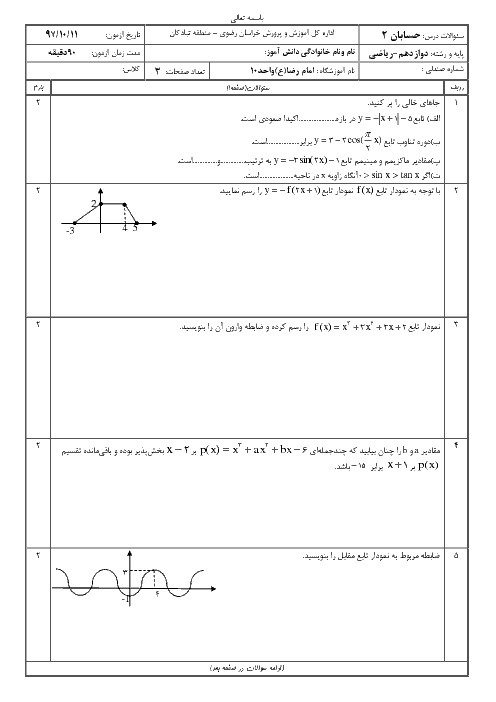
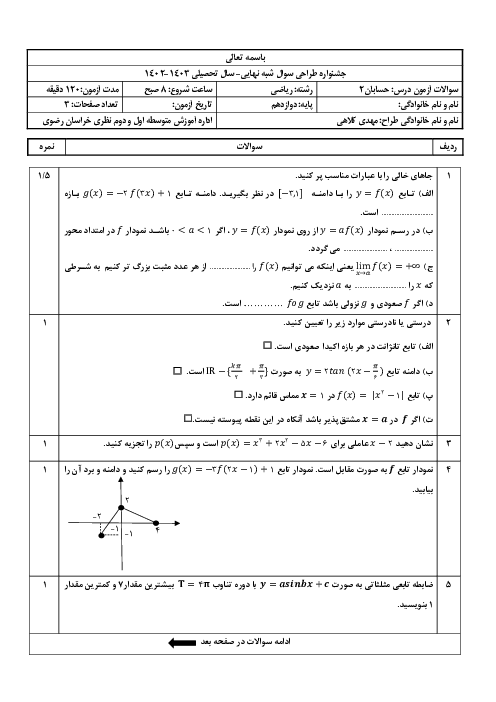
فرم معتبر نیست.
درس 1: اکسترممهای یک تابع و توابع صعودی و نزولی
حسابان (2)
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
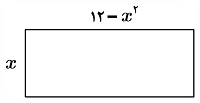
ماکزیمم مقدار مساحت مستطیل به ابعاد x و $12 - {x^2}$ را به دست آورید.
پاسخ تشریحی :
نمایش پاسخ
$S(x) = x(12 - {x^2}) = - {x^3} + 12x$
$S'(x) = - 3{x^2} + 12 = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{x = - 2} \\
{x = + 2}
\end{array}} \right.$
$\xrightarrow{{x \in [0,\sqrt {12} ]}}x = 2 \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{S(0) = S(\sqrt {12} ) = 0} \\
{S(2) = 16 = \max }
\end{array}} \right.$
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...