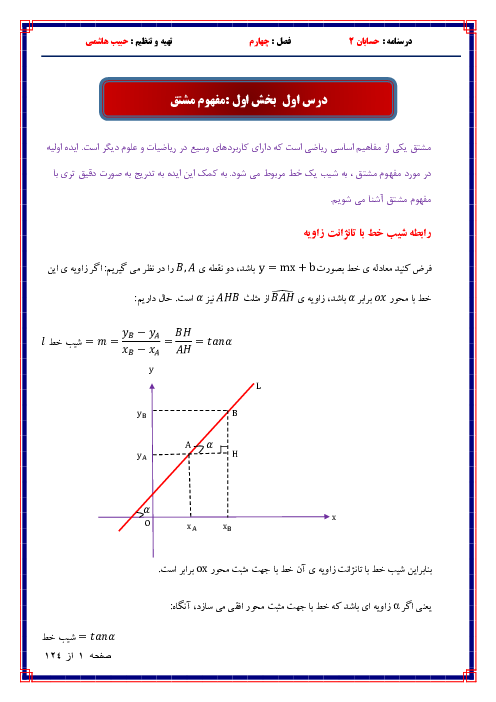
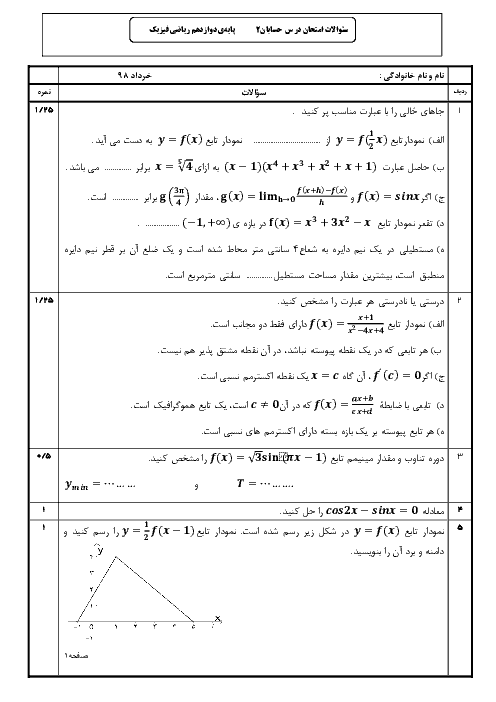
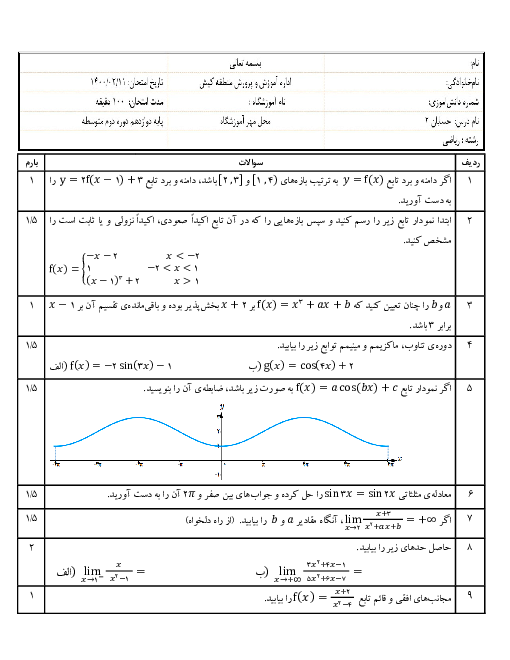
با توجه به ثابت بودن کل مساحت سطح محصور بین نمودار تابع و محور $x$ها، برای آن که مساحت قسمت هاشور خورده، کم‌ترین مقدار ممکن شود، لازم است که مساحت مثلث $OAB$ بیش‌ترین مقدار باشد.

اگر مختصات رأس $A$ از مثلث را $(x,y)$ در نظر بگیریم، قاعدهٔ مثلث $(AB)$ برابر $2x$ و ارتفاع مثلث $(OH)$ برابر $y$ خواهد بود. پس مساحت این مثلث متساوی‌الساقین برابر است با، 

$\begin{align}  & S=\frac{1}{2}(AB)(OH)=\frac{1}{2}(2x)(y)=xy \\  & \Rightarrow S(x)=x\sqrt{2-{{x}^{2}}} \\  & \Rightarrow S'(x)=0\Rightarrow 1\times \sqrt{2-{{x}^{2}}}+\frac{-2x}{2\sqrt{2-{{x}^{2}}}}\times x=0 \\  & \Rightarrow x=\pm 1\xrightarrow[mokhtasat\,ast]{''A''\,dar\,moraba\,aval}x=1 \\  & \Rightarrow OH=y=\sqrt{2-{{x}^{2}}}\xrightarrow{x=1}y=1 \\ \end{align}$

حال از آن‌جا که در مثلث متساوی‌الساقین، میانه و ارتفاع وارد بر قاعده بر هم منطبق‌اند، مقدار میانه نیز برابر $1$ خواهد بود.