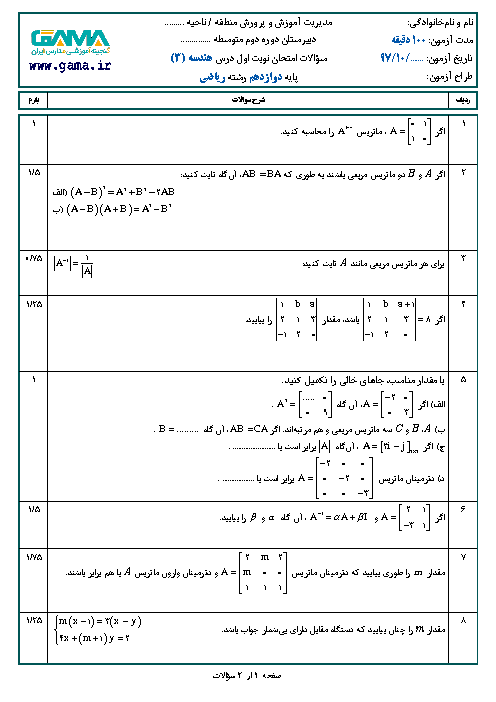
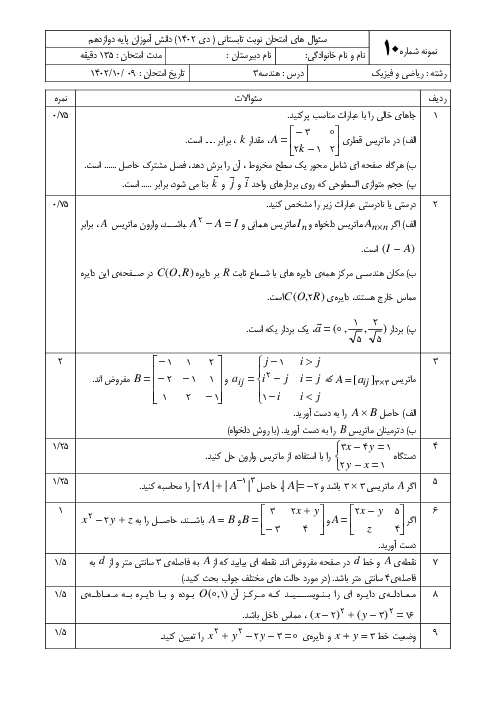
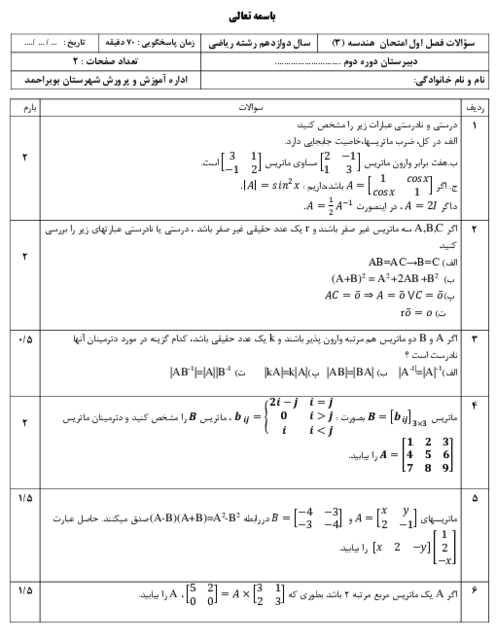
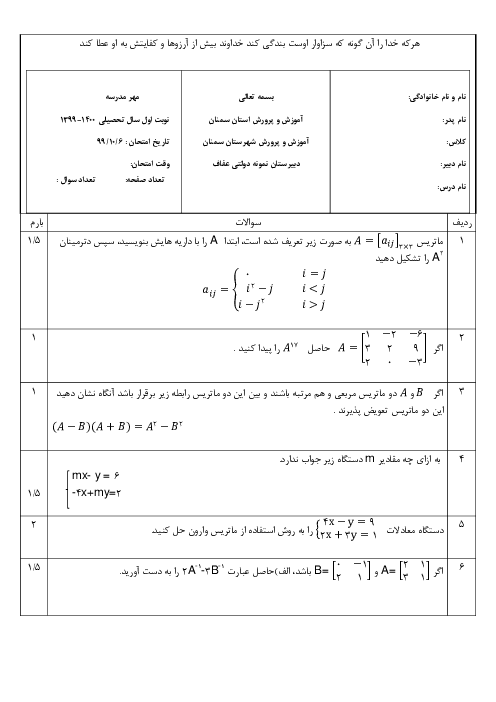
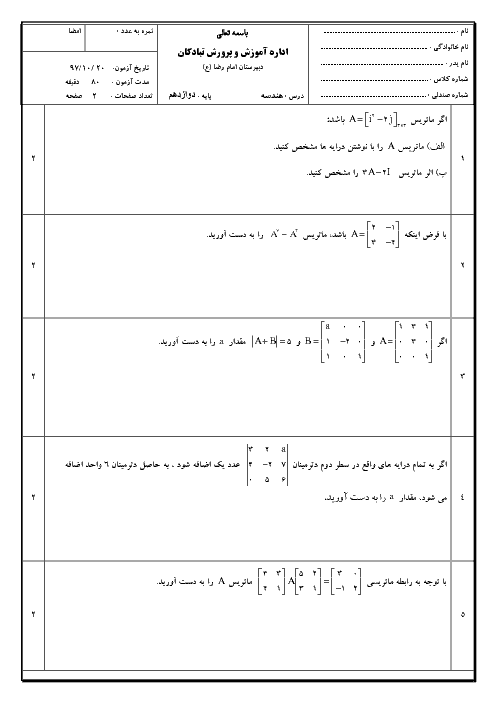
نکته $:\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\operatorname{Cos}\theta \,\,\,,\,\,\,\left| \overrightarrow{a}\times \overrightarrow{b} \right|=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\operatorname{Sin}\theta $

با توجه به اطلاعات سؤال و نکته داریم:

$\begin{align}
  & (a.b)\left| a\times b \right|=9\sqrt{3}\Rightarrow {{\left| a \right|}^{2}}{{\left| b \right|}^{2}}\operatorname{Cos}\theta \operatorname{Sin}\theta =4\times 9\times \frac{1}{2}\operatorname{Sin}2\theta =9\sqrt{3}\Rightarrow \operatorname{Sin}2\theta =\frac{\sqrt{3}}{2} \\ 
 & \Rightarrow \left\{ \begin{matrix}
   2\hat{\theta }={{60}^{{}^\circ }}\Rightarrow \hat{\theta }={{30}^{{}^\circ }}  \\
   2\hat{\theta }={{120}^{{}^\circ }}\Rightarrow \hat{\theta }={{60}^{{}^\circ }}  \\
\end{matrix} \right. \\ 
\end{align}$

حال مساحت مثلث بناشده بر این دو بردار را به‌دست می‌آوریم:

$\left\{ \begin{matrix}
   S=\frac{1}{2}\left| a\times b \right|=\frac{1}{2}\left| a \right|\left| b \right|\operatorname{Sin}\theta =\frac{1}{2}\times 2\times 3\times \frac{1}{2}=\frac{3}{2}  \\
   S=\frac{1}{2}\left| a\times b \right|=\frac{1}{2}\left| a \right|\left| b \right|\operatorname{Sin}\theta =\frac{1}{2}\times 2\times 3\times \frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}  \\
\end{matrix} \right.$

با توجه به گزینه‌ها، گزینه‌ی 3 پاسخ است.