درس 1: مفاهیم اولیه و زاویهها در دایره
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
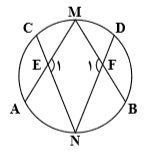
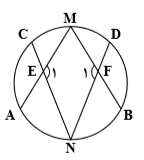
در شکل مقابل، $\overset\frown{AC}+\overset\frown{BD}={{98}^{\circ }}$، اندازهٔ ${{\hat{E}}_{1}}+{{\hat{F}}_{1}}$ کدام است؟
1 )
${{131}^{\circ }}$
2 )
${{219}^{\circ }}$
3 )
${{242}^{\circ }}$
${{229}^{\circ }}$
پاسخ تشریحی :