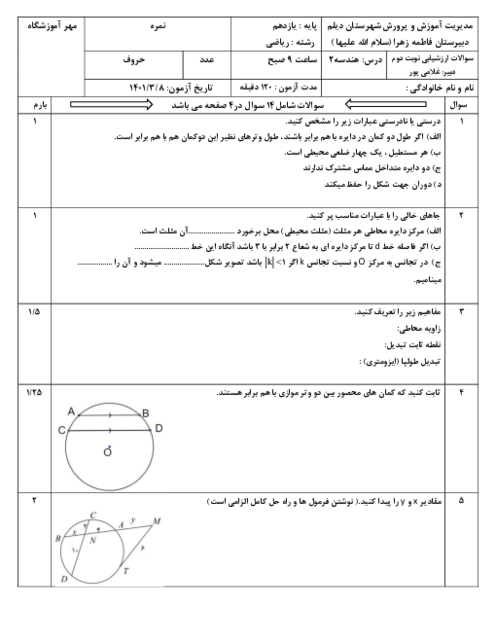
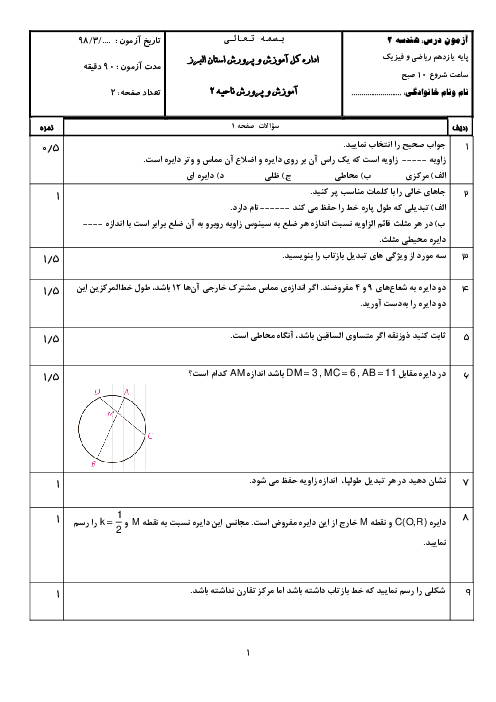
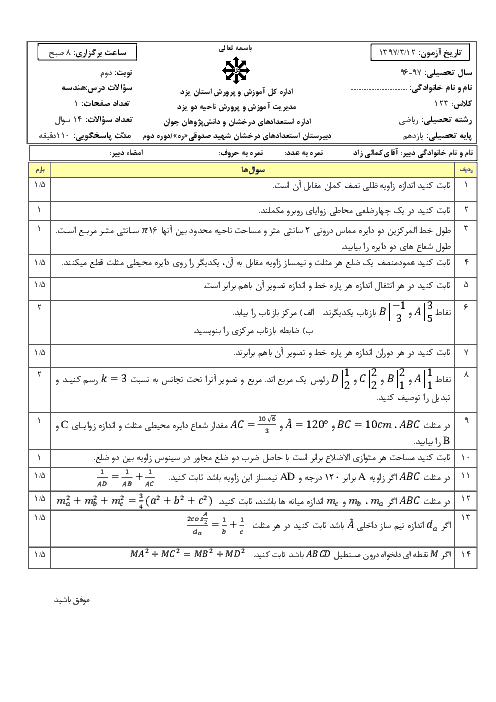
درس 1: مفاهیم اولیه و زاویهها در دایره
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
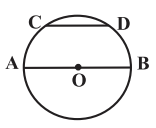
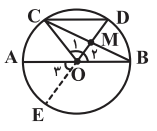
در شكل مقابل O مركز دايره میباشد. اگر CD موازی AB و نصف آن باشد و نقطهٔ تلاقی BC و OD را M بناميم، در اين صورت اندازهٔ زاويهٔ BMD كدام است؟