قسمت 1 - صفحه 48 تا 56 - مفهوم جزء اعشاری یک عدد با استفاده از تابع جزء صحیح

قسمت 2 - صفحه 48 تا 56 - کاربرد مفهوم تابع ثابت در حل مسائل تابع

قسمت 3 - صفحه 48 تا 56 - طریقهی بازه بندی در رسم توابع جزء صحیح

قسمت 4 - صفحه 48 تا 56 - مفهوم تابع از طریق ضابطه

قسمت 5 - صفحه 48 تا 56 - محاسبهی برد توابع براکت (جزء صحیح)

قسمت 6 - صفحه 48 تا 56 - نحوهی رسم ترکیبی توابع براکتی و قدر مطلقی

قسمت 7 - صفحه 48 تا 56 - نحوهی رسم نمودار تابع براکت x

قسمت 8 - صفحه 48 تا 56 - نحوهی رسم نمودار جزء اعشاری x

قسمت 9 - صفحه 48 تا 56 - نحوهی رسم نمودار براکت x و براکت x-

قسمت 10 - صفحه 48 تا 56 - نحوهی رسم نمودار براکت ax

قسمت 11 - صفحه 48 تا 56 - شرط پرش توابع جزء صحیح در یک نقطه

قسمت 12 - صفحه 48 تا 56 - رسم نمودار توابع براکت

قسمت 13 - صفحه 48 تا 56 - ویدیوی برد تابع جزء صحیح

قسمت 14 - صفحه 48 تا 56 - خواص تابع جزء صحیح (براکت)

قسمت 15 - صفحه 48 تا 56 - حل سوالات چهارگزینهای تابع جزء صحیح (براکت)

قسمت 16 - صفحه 48 تا 56 - آموزش مفهومی تابع جزء صحیح (براکت)

قسمت 17 - صفحه 48 تا 56 - برد تابع آبشاری

قسمت 19 - صفحه 48 تا 56 - ویدیوی آموزش حرفهای رسم تابع گلدانی

قسمت 20 - صفحه 48 تا 56 - ویدیوی آموزش تساوی دو تابع

قسمت 21 - صفحه 48 تا 56 - برد توابع جزء صحیح (توابع داخل براکت)

قسمت 22 - صفحه 48 تا 56 - ویدیوی محاسبهی برد توابع گویا

قسمت 23 - صفحه 48 تا 56 - ویدیوی برد توابع گویا و رادیکالی

طول پاره خط حاصل از امتداد نیمسازهای داخلی مثلث متساوی الساقین

تدریس فشرده تابع پله ای و تابع جزء صحیح
حل نمونه سوال شبه نهایی ریاضی 2 یازدهم (سری 2)
حل تمرینهای صفحه 18: سهمی، معادلات درجه دوم، نقاط مینیمم و ماکزیمم | ریاضی 2 تجربی

دوره جمع بندی شب امتحان فصل هفتم ریاضی یازدهم تجربی
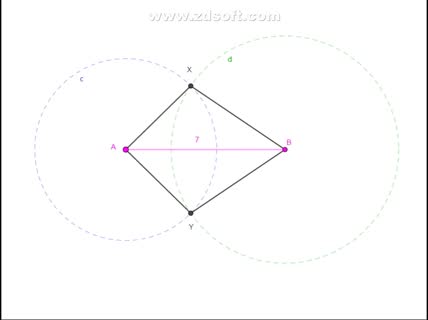
صفحه 26 کتاب درسی: رسم مثلث با داشتن اندازه سه ضلع (سوال 6 قسمت ب)

مفهوم تابع از طریق ضابطه
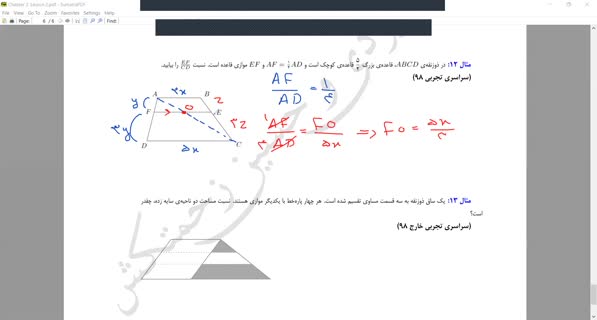
ویدیوی حل 2 تست کنکوری از قضیهٔ تالس در ذوزنقه
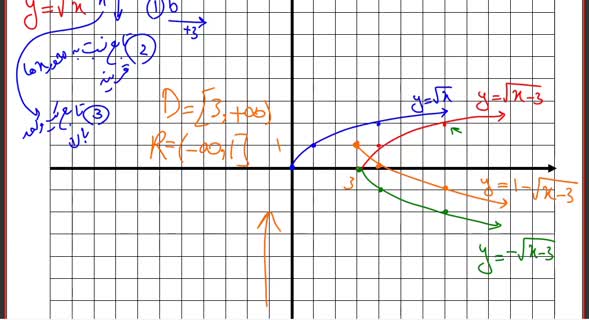
حل سوالات امتحان نهایی ریاضی 2 یازدهم تجربی نوبت صبح خرداد 1402

تشابه مثلث ها و قضیه اساسی تشابه مثلث ها
موارد مشابه بیشتر
ویدیوی آموزش رسم تابع سرسره ای (آبشاری) f(x) = |x-a|-|x-b|
باز نشر محتواها در فضای مجازی، ممنوع است.