درس 3: آهنگ متوسط تغییر و آهنگ لحظه‌ای تغییر
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
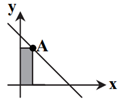
نقطۀ $A$ روی خط $y=4-2x$ در ناحيۀ اول مطابق شكل قرار گرفته است. مساحت مستطيل را به صورت تابعی برحسب طول نقطۀ $A$ نوشته‌ايم. آهنگ تغيير لحظه‌ای مساحت مستطيل وقتی طول نقطۀ $A$ برابر $\frac{1}{2}$ باشد، كدام است؟
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...