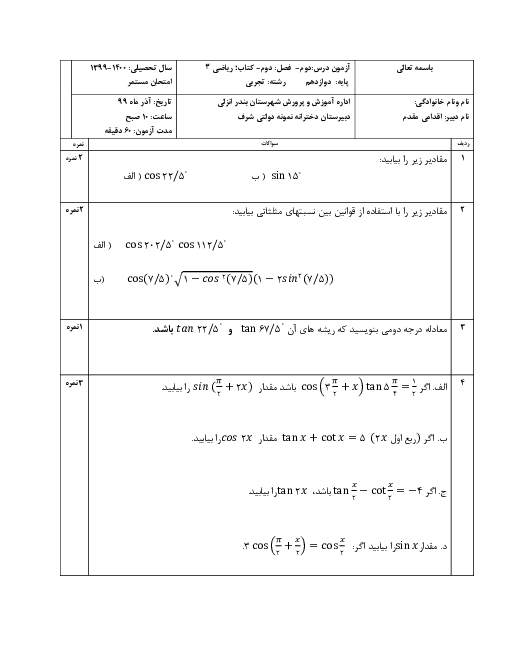
ابعاد مستطیلی با بیشترین مساحت را تعیین کنید به طوری که مطابق شکل، دو ضلع آن روی محورهای مختصات و یک رأس آن روی مبدأ و رأس دیگر آن روی منحنی $y = {(x - 2)^2}$ قرار داشته باشد.
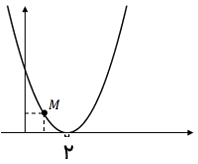
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!