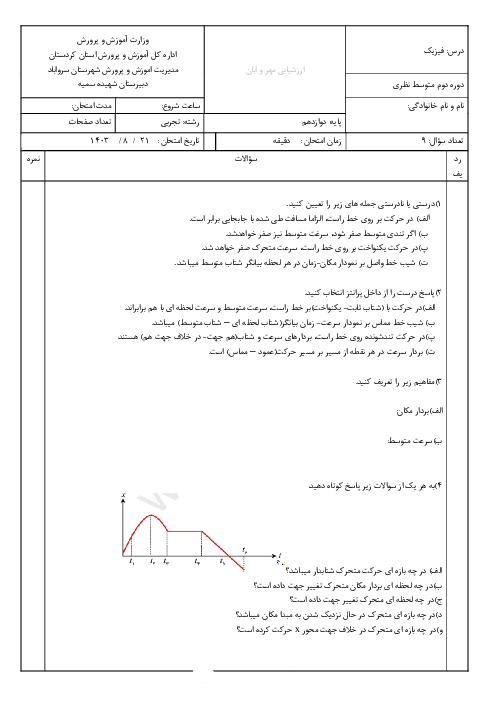
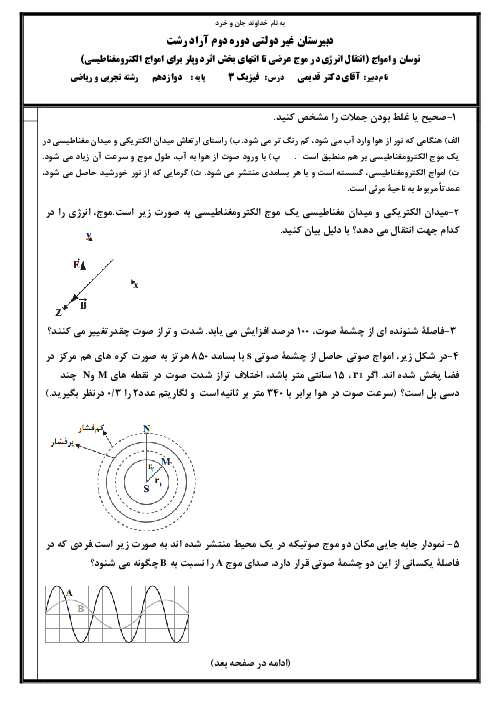
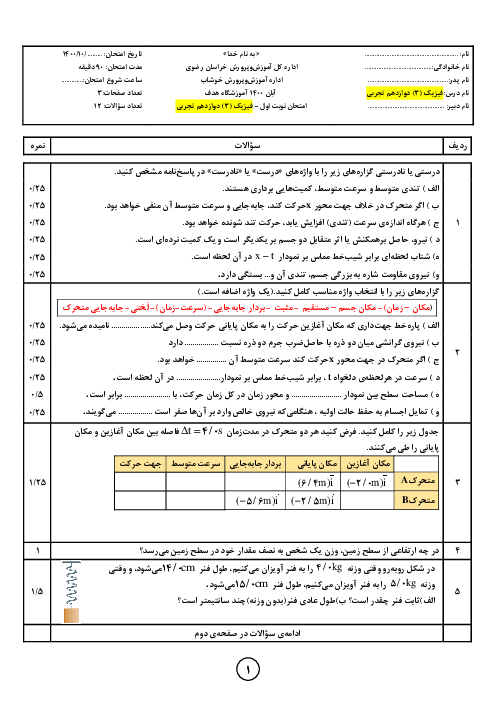
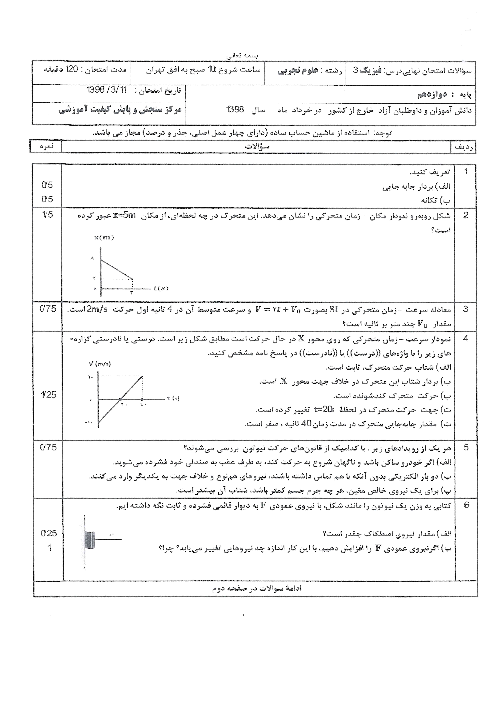
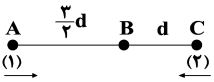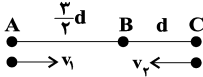با توجه به رابطۀ جابه‌جایی در حرکت یکنواخت داریم:

$\Delta x=vt\left\{ \begin{matrix}
   \Delta {{x}_{1}}=\frac{3}{2}d,{{t}_{1}}=4s\Rightarrow \frac{3}{2}d=4{{v}_{1}}\Rightarrow {{v}_{1}}=\frac{3}{8}d  \\
   \Delta {{x}_{2}}=d,{{t}_{2}}=4s\Rightarrow d=4{{v}_{2}}\Rightarrow {{v}_{2}}=\frac{d}{4}  \\
\end{matrix} \right.$

اگر ${t}'$ مدت زمانی باشد که طول می‌کشد تا متحرک اول از B به C برسد و ${t}''$ مدت زمانی باشد که طول می‌کشد تا متحرک دوم از B به A برسد، داریم:

$\begin{align}
  & {{v}_{1}}{t}'=\overline{BC}\xrightarrow[{{v}_{1}}=\frac{3}{8}d]{\overline{BC}=d}{t}'=\frac{8}{3}s \\ 
 & {{v}_{2}}{t}''=\overline{AB}\xrightarrow[\left| {{v}_{2}} \right|=\frac{d}{4}]{\overline{AB}=\frac{3}{2}d}{t}''=6s \\ 
 & \Rightarrow {t}''-{t}'=6-\frac{8}{3}=\frac{10}{3}s \\ 
\end{align}$