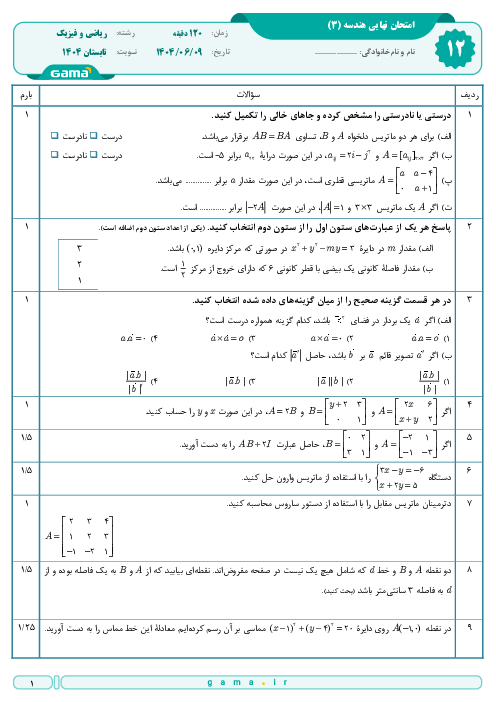
فاصلهٔ دو کانون برابر با فاصلهٔ کانونی بیضی است، پس:

 $2c=5-(-5)=10\Rightarrow c=5$

 می‌دانیم مجموع فواصل هر نقطه روی بیضی از دو کانون برابر با طول قطر بزرگ بیضی $(2a)$ است؛ یعنی:

 $\begin{align}
  & PF+P{F}'=2a \\
 & \Rightarrow \sqrt{{{(2-0)}^{2}}+{{(-5-6)}^{2}}}+\sqrt{{{(2-0)}^{2}}+{{(5-6)}^{2}}}=2a \\
 & \Rightarrow \sqrt{125}+\sqrt{5}=2a\Rightarrow 5\sqrt{5}+\sqrt{5}=2a \\
 & \Rightarrow a=3\sqrt{5} \\
\end{align}$

با قرار دادن مقادیر $a$ و $c$ در رابطهٔ ${{a}^{2}}-{{c}^{2}}={{b}^{2}}$ مقدار $b$ به دست می‌آید.

 ${{(3\sqrt{5})}^{2}}-{{5}^{2}}={{b}^{2}}\Rightarrow {{b}^{2}}=20\Rightarrow b=2\sqrt{5}$

طول وتر کانونی بیضی برابر با $\frac{2{{b}^{2}}}{a}$ است. بنابراین:

 $\frac{2\times 20}{3\sqrt{5}}$

مساحت مثلث برابر است با:

${{S}_{\overset{\Delta }{\mathop FMN}\,}}=\frac{MN\times F{F}'}{2}=\frac{\frac{40}{3\sqrt{5}}\times (2\times 5)}{2}=\frac{40\sqrt{5}}{3}$