درس 2: وارون یک تابع و تابع یک به یک
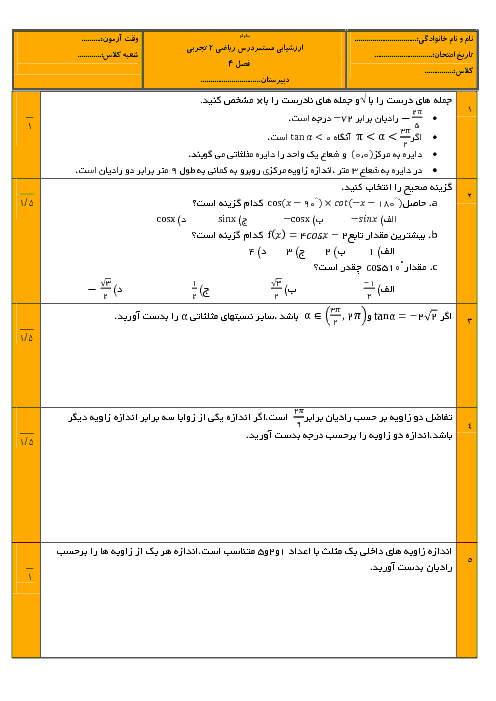
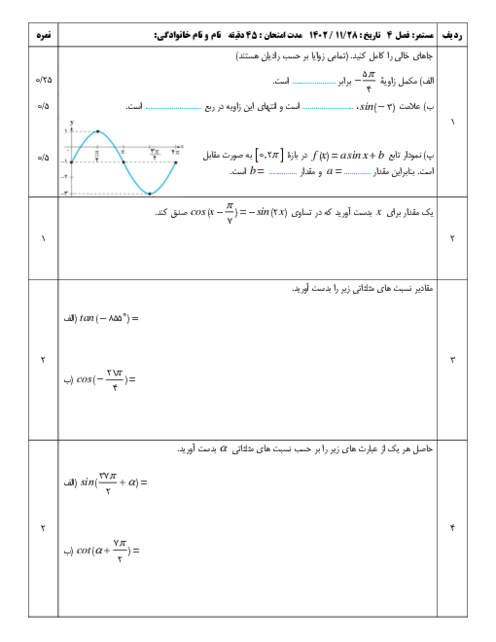
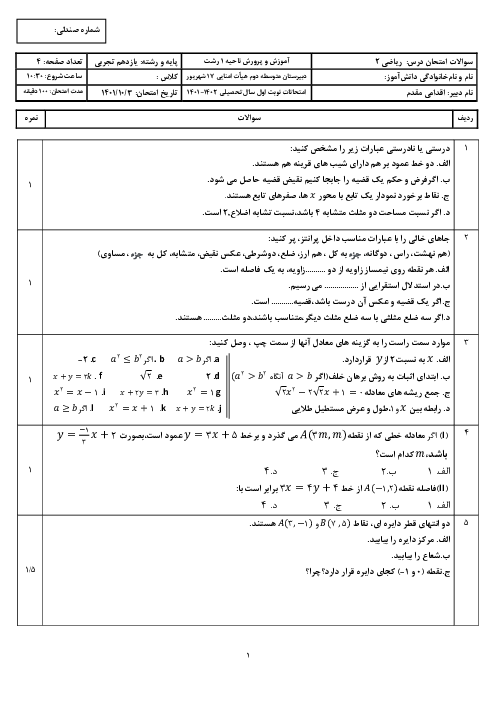
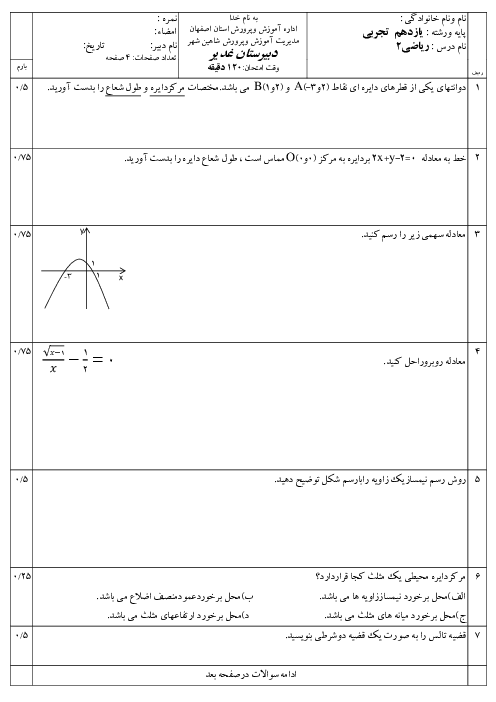
ریاضی (2)
یازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
تابع درجه دوم $f(x)=3{{x}^{2}}+12x+13$ با کدام‌یک از شرط‌های زیر وارون‌پذیر می‌شود؟
1 )
$x\in \left( -\infty ,0 \right]$
2 )
$\left| x \right|\ge 2$
$x+3\le 0$
4 )
$-3\le x\le 3$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...