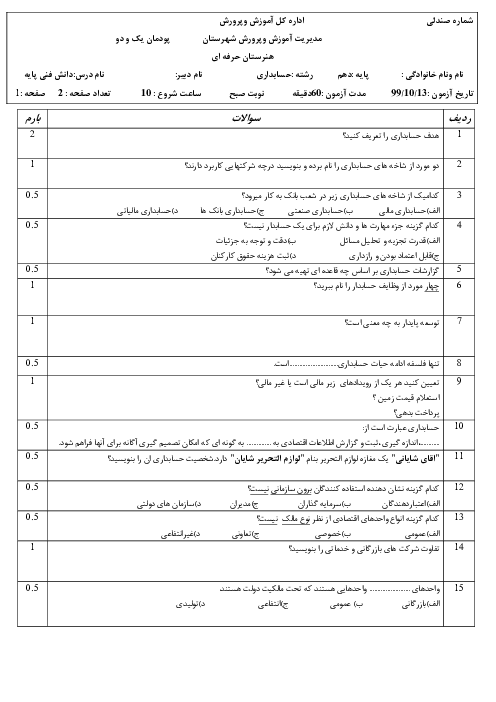
اگر $\sum\limits_{{}}^{{}}{y_{i}^{2}}=1375\,\,,\,\,\sum\limits_{{}}^{{}}{x_{i}^{2}}=360\,\,,\,\,\sum\limits_{{}}^{{}}{{{x}_{i}}}{{y}_{i}}=500\,\,,\,\,\,\sum\limits_{{}}^{{}}{{{y}_{i}}}=75\,\,\,,\,\,\,\sum\limits_{{}}^{{}}{{{x}_{i}}}=40\,\,,\,\,n=5$ باشد، ضریب همبستگی کدام است؟
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...