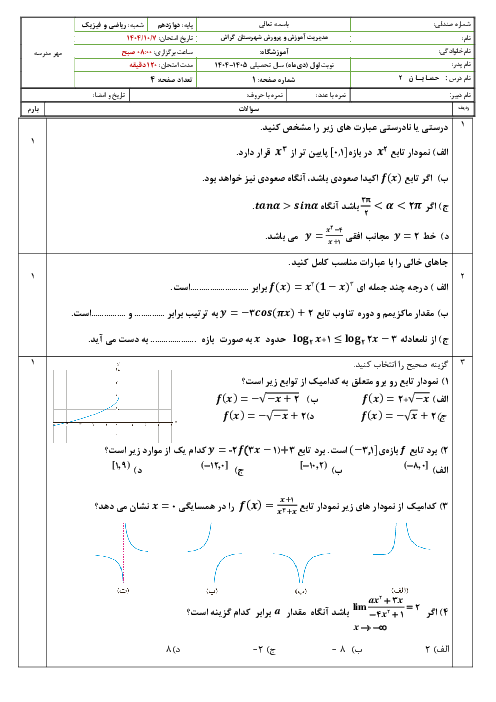
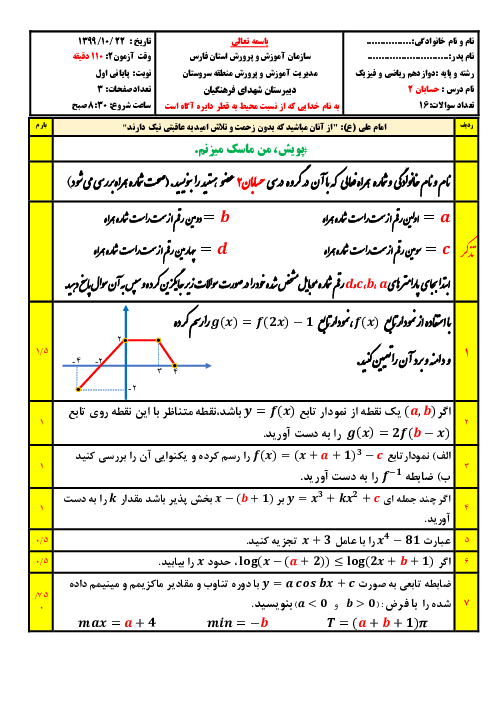
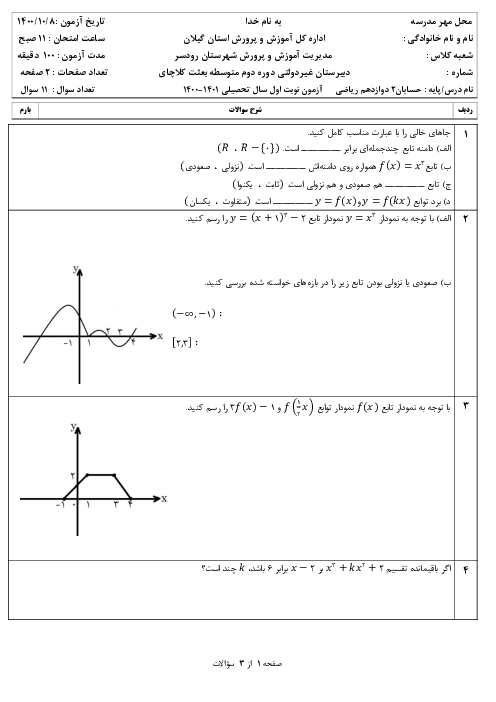
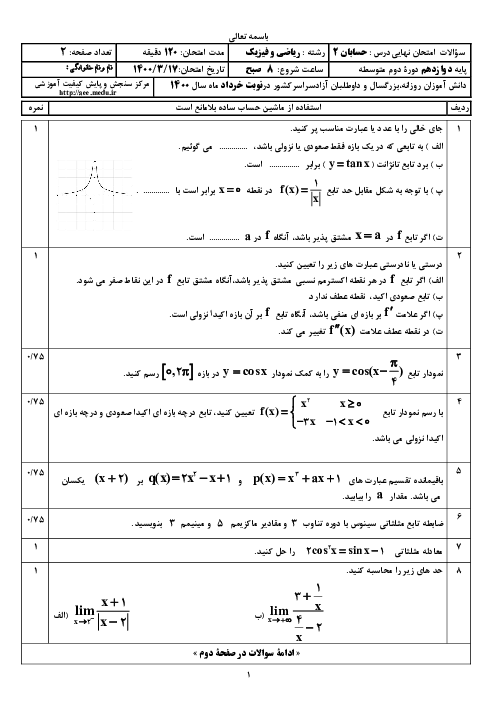
در تابع $f(x)=\left\{ \begin{matrix} \left[ \frac{2}{x} \right]{{\sin }^{2}}x\,\,\,\,;x\ne 0 \\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;x=0 \\ \end{matrix} \right.$، مقدار ${f}'(0)$ کدام است؟ ($\left[ \, \right]$، علامت جزء صحیح است.)
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...