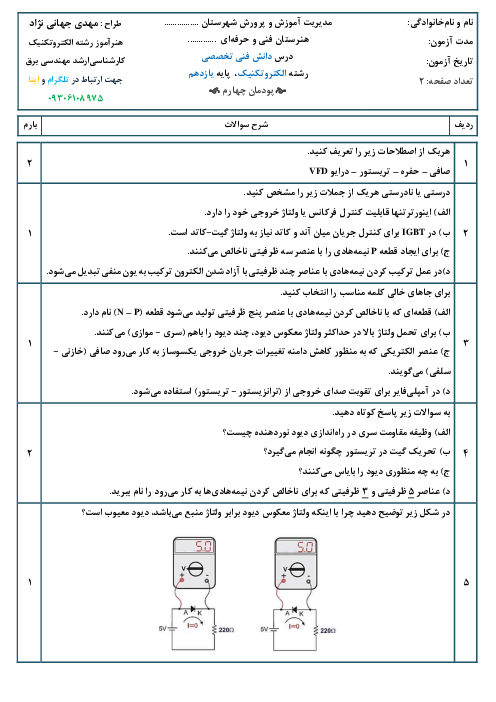
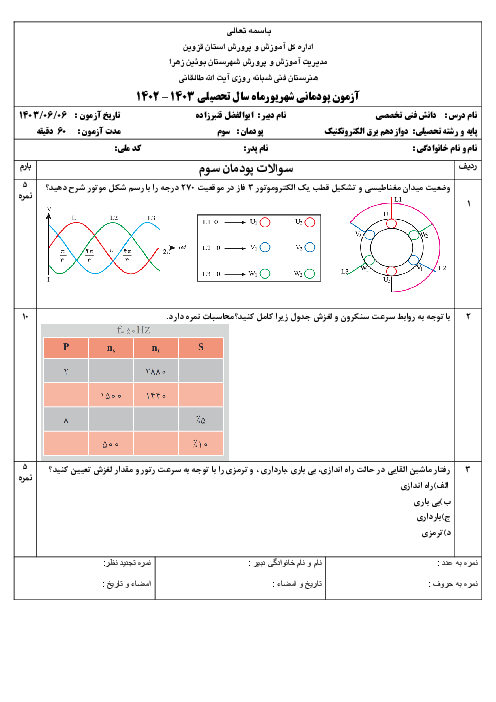
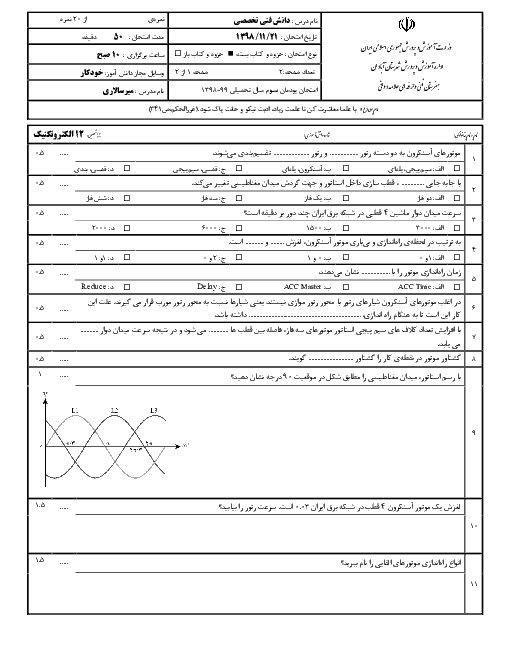
$\varphi =-{{37}^{\circ }}$

${{I}_{e}}=\frac{5}{\sqrt{2}}=\frac{5}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}=\frac{5}{2}\sqrt{2}\left( A \right)$

${{V}_{e}}=\frac{200}{\sqrt{2}}=100\sqrt{2}\left( v \right)$

$P={{V}_{e}}.{{I}_{e}}\times \cos \varphi =\frac{5}{2}\sqrt{2}\times 100\sqrt{2}\times \cos -{{37}^{\circ }}=500\times 0/8=400\left( w \right)$

$P=RI_{e}^{2}\to 400=R\times {{\left( \frac{5}{2}\sqrt{2} \right)}^{2}}\Rightarrow R=\frac{400}{\frac{25}{2}}=\frac{800}{25}$

$R=32\left( \Omega  \right)$

$Q={{V}_{e}}.{{I}_{e}}.\sin \varphi ={{X}_{C}}.I_{e}^{2}$

$Q=100\sqrt{2}\times \frac{5}{2}\sqrt{2}\times \sin \left( -{{37}^{\circ }} \right)=500\times 0/6=300\left( w \right)$

$300={{X}_{C}}\times \frac{25}{2}\to {{X}_{C}}=\frac{300}{\frac{25}{2}}=\frac{600}{25}=24\left( \Omega  \right)$

${{X}_{C}}=\frac{1}{\omega .C}\to C=\frac{1}{\omega .{{X}_{C}}}=\frac{1}{200\times 24}=\frac{{{10}^{-2}}}{48}$

$C=\frac{{{10}^{-2}}}{48}\times {{10}^{+6}}\times {{10}^{-6}}=\frac{{{10}^{4}}}{48}\mu F=208/4\mu F$