چه تعداد از عبارات زیر صحیح است؟ - هر دو مستطیل دلخواه متشابه‌اند. - هر دو مثلث متساوی‌الساقین که یک رأس قائمه دارند، متشابه‌اند. - هر دو مثلث متشابه، هم‌نهشت هستند.…

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

** فصل 3: استدلال و اثبات در هندسه ریاضی نهم دوره اول متوسطه درسنامه آموزشی این مبحث

چه تعداد از عبارات زیر صحیح است؟

- هر دو مستطیل دلخواه متشابه‌اند.

- هر دو مثلث متساوی‌الساقین که یک رأس قائمه دارند، متشابه‌اند.

- هر دو مثلث متشابه، هم‌نهشت هستند.

- چهارضلعی که هر دو زاویهٔ مجاور آن، مکمل باشند، یک متوازی‌الاضلاع است.

1 )

2 )

3 )

4 )

نمایش پاسخ

بررسی عبارت‌ها

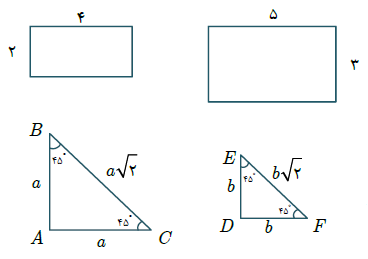
در تشابه شرط لازم برابری زوایا و شرط کافی برابری نسبت اضلاع متناظر است. در عبارت اول به مثال نقض توجه کنید.

$\frac{4}{5} \ne \frac{2}{3} \Rightarrow $ متشابه نیستند

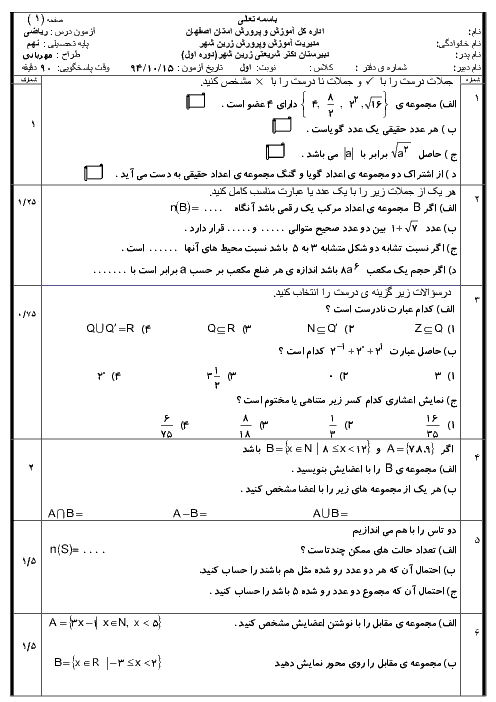
در مثلث قائم‌الزاویه متساوی الساقین ABC و DEF دلخواه در نظر می‌گیریم. چون مثلث‌ها قائم‌الزاویه و متساوی الساقین هستند پس زوایای تند باهم برابرند و از طرفی نسبت اضلاع برابر است.

$\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} \Rightarrow \frac{a}{b} = \frac{a}{b} = \frac{{a\sqrt 2 }}{{b\sqrt 2 }} = \frac{a}{b}$ پس متشابه‌اند

طبق مثال بالا تشابه لزوماً همنهشتی را نتیجه نمی‌دهد چون برابری اضلاع وجود ندارد.

عبارت چهارم را می‌توان ثابت نمود اگر چنین شرایطی برقرار باشد به اینصورت اضلاع روبه‌رو موازی هستند در نتیجه متوازی الاضلاع است.