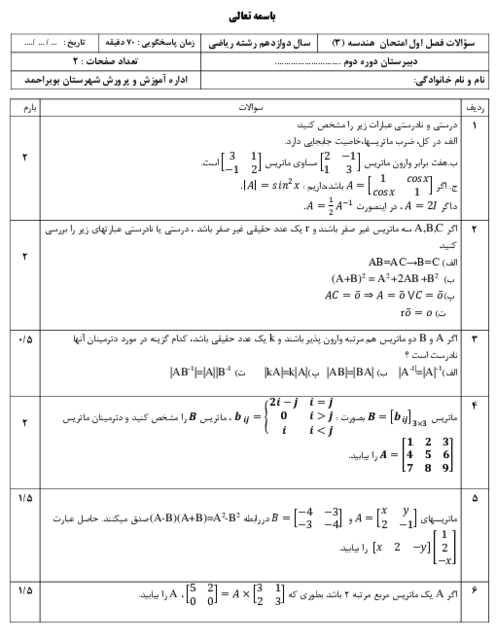
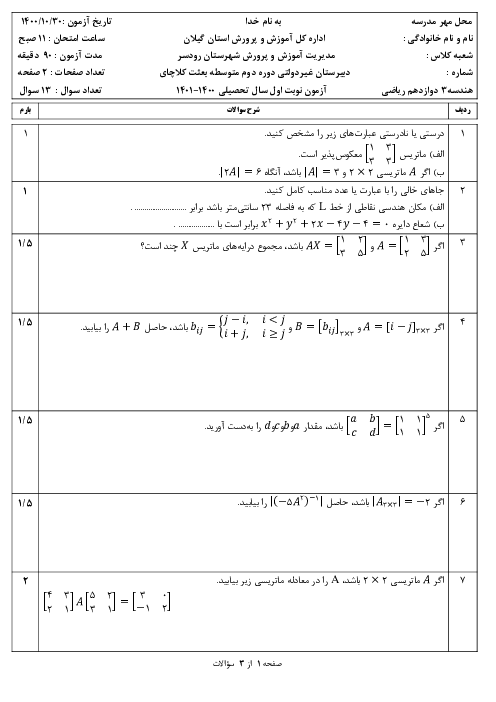
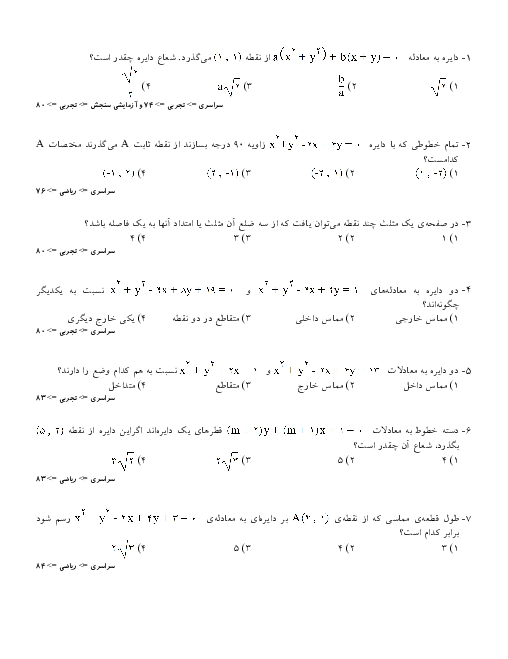
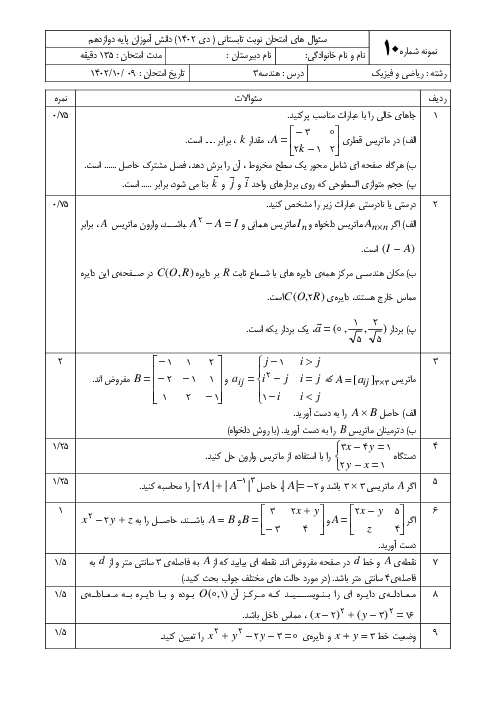
$\overrightarrow{a}-\overrightarrow{b}$ و $\overrightarrow{b}$ را به دست میآوریم و از رابطهٔ $\cos \theta =\frac{\overrightarrow{u}.\overrightarrow{v}}{\left| \overrightarrow{u} \right|\left| \overrightarrow{v} \right|}$، کسینوس زاویهٔ بین دو بردار را مییابیم.
$\overrightarrow{a}-\overrightarrow{b}=(2,3,1)-(1,-1,1)=(1,4,0)$
بنابراین کسینوس زاویهٔ بین $\overrightarrow{a}-\overrightarrow{b}$ و $\overrightarrow{b}$ برابر میشود با:
$\begin{align} & \cos \theta =\frac{(\overrightarrow{a}-\overrightarrow{b}).\overrightarrow{b}}{\left| \overrightarrow{a}-\overrightarrow{b} \right|\left| \overrightarrow{b} \right|}=\frac{(1,4,0).(1,-1,1)}{\sqrt{{{1}^{2}}+{{4}^{2}}+{{0}^{2}}}\sqrt{{{1}^{2}}+{{(-1)}^{2}}+{{1}^{2}}}} \\ & =\frac{1-4+0}{\sqrt{17}\sqrt{3}}=-\sqrt{\frac{3}{17}} \\ \end{align}$