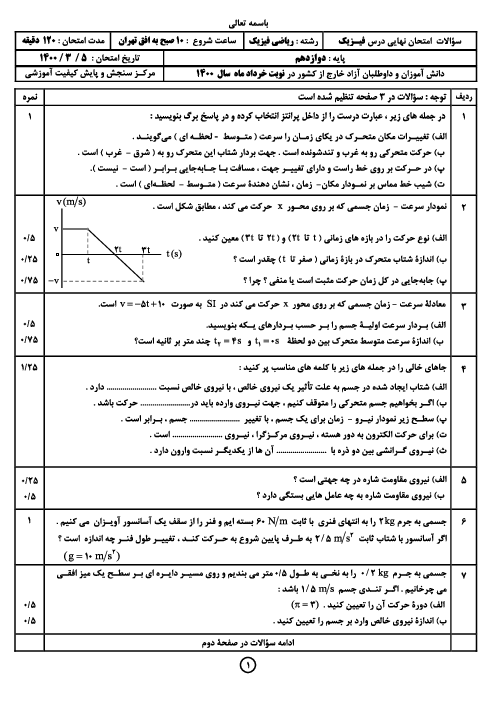
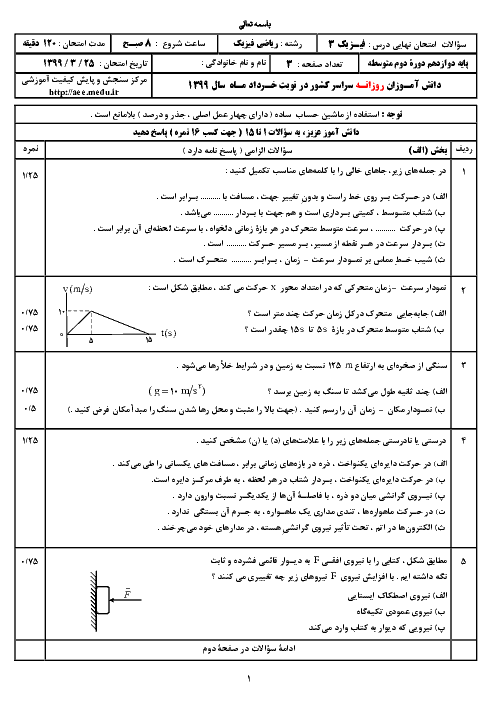
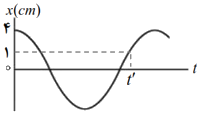
شکل زیر نمودار مکان ـ زمان نوسانگر جرم ـ فنری را نشان میدهد. اگر جرم وزنه 200g و اندازهٔ شتاب نوسانگر در لحظهٔ ${t'}$ برابر $4\frac{m}{{{s^2}}}$ باشد، انرژی پتانسیل نوسانگر در نقاط بازگشتی چند ژول است؟ (از نیروهای اتلافی چشمپوشی شود)
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...