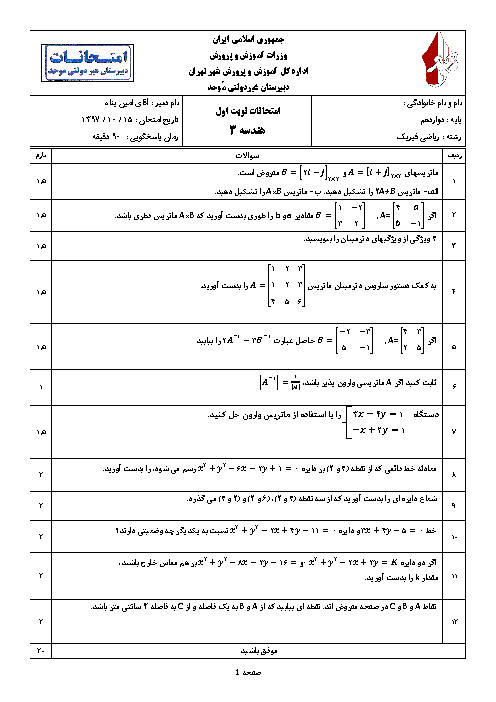
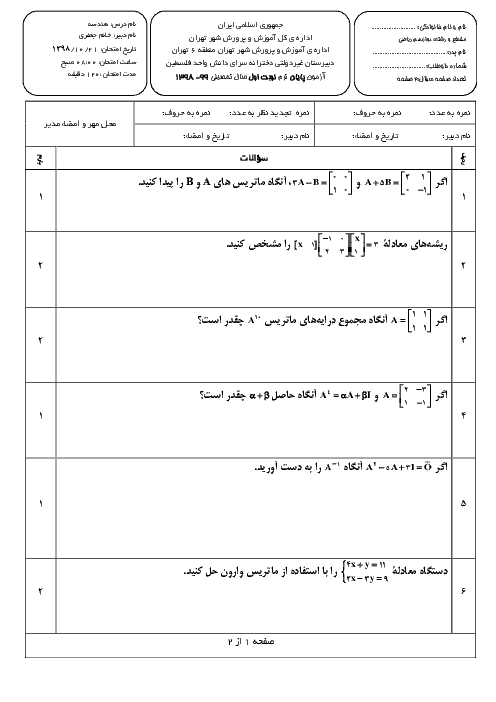
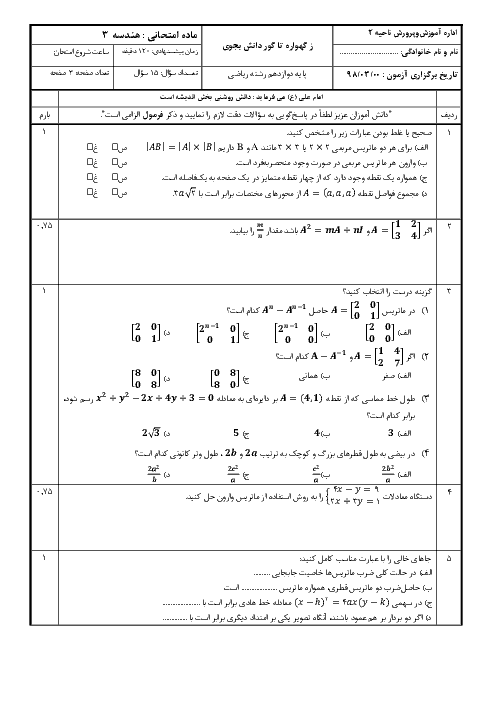
اگر نقطهٔ $A=(a,b,c)$ را روی صفحهٔ $xy$ و روی محور $z$ها تصویر کنیم، به‌ترتیب نقاط $B$ و $C$ به‌دست می‌آید. بین طول پاره‌خط‌های $BC$ و $OA$ کدام رابطه همواره برقرار است؟ ($O$ مبدأ مختصات است.)
1 )
$\left| BC \right|=2\left| OA \right|$
2 )
$\left| OA \right|=2\left| BC \right|$
3 )
$\left| OA \right|+\left| BC \right|=2$
$\left| OA \right|=\left| BC \right|$
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...