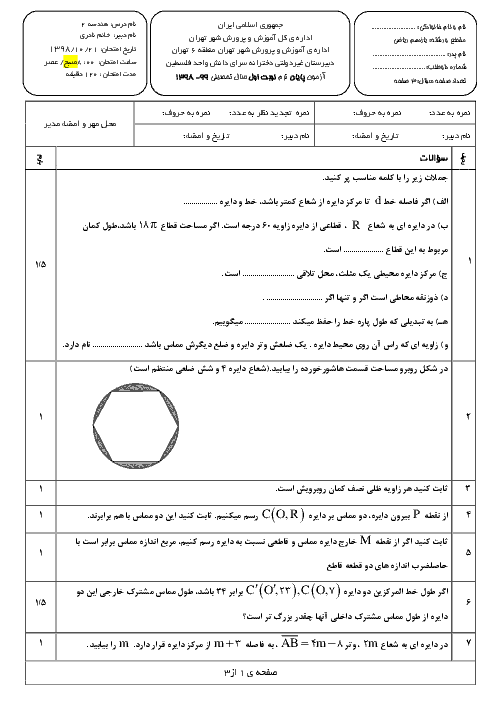
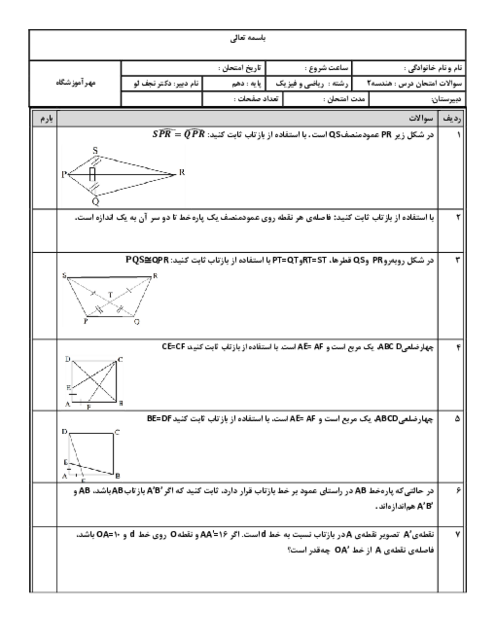
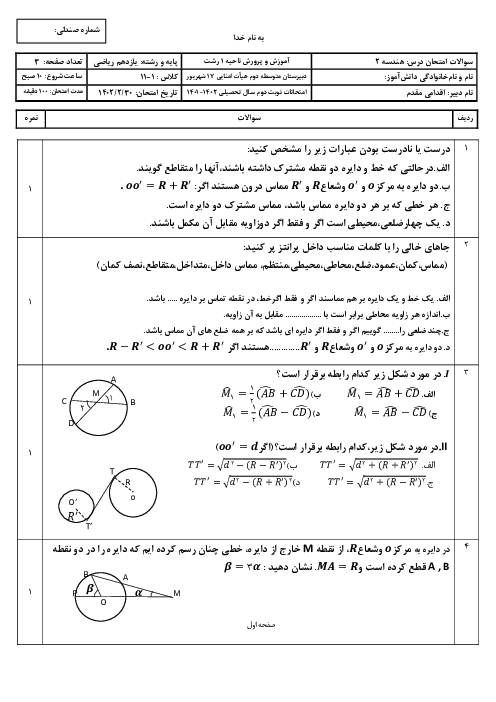
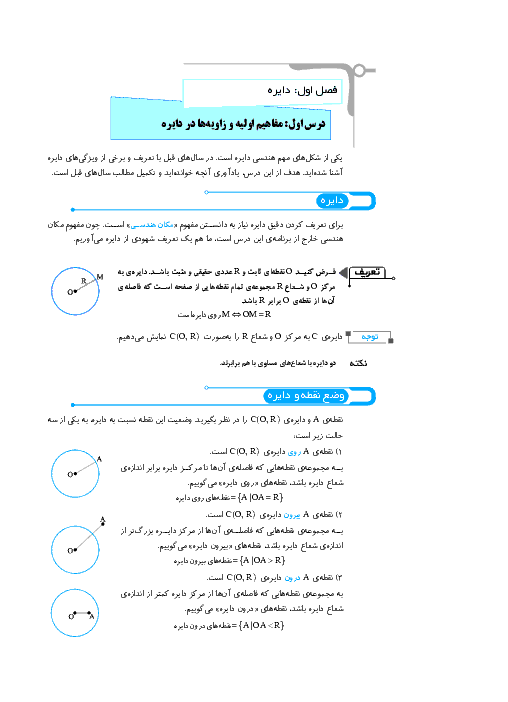
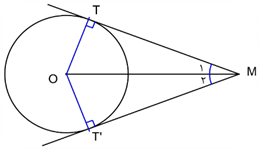
هرگاه از نقطهٔ M خارج دایرهٔ $C(O,R)$ دو مماس بر دایره رسم کنیم و T و $T'$ نقاط تماس باشند، ثابت کنید:
الف) اندازههای دو مماس باهم برابرند.
ب) OM نیمساز $\widehat {TMT'}$ است.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!