تابع در بازهٔ اكيداً نزولی با تقعر رو به پايين است. حداكثر مقدار كدام است؟ | حسابان (2) دوازدهم شماره 91504 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت اول گام به گام کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

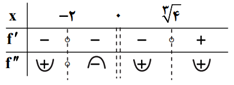
درس 2: جهت تقعر نمودار یک تابع و نقطۀ عطف آن حسابان (2) دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

تابع $f(x)={{x}^{2}}+\frac{8}{x}$ در بازهٔ $(a,b)$ اكيداً نزولی با تقعر رو به پايين است. حداكثر مقدار $b-a$ كدام است؟

1 )

$\sqrt[3]{4}$

2 )

2

3 )

$2+\sqrt[3]{4}$

4 )

4

نمایش پاسخ

ابتدا مشتق اول و سپس مشتق دوم را به‌دست آورده و تعیین علامت می‌کنیم.

${f}'(x)=2x-\frac{8}{{{x}^{2}}}\Rightarrow {f}'(x)=0\Rightarrow \frac{2{{x}^{3}}-8}{{{x}^{2}}}=0\Rightarrow 2{{x}^{3}}=8\Rightarrow x=\sqrt[3]{4}$

${f}''(x)=2+\frac{16}{{{x}^{3}}}\Rightarrow {f}''(x)=0\Rightarrow \frac{2{{x}^{3}}+16}{{{x}^{3}}}=0\Rightarrow 2{{x}^{3}}=-16\Rightarrow x=-2$

ما به دنبال بازه‌ای هستیم که در آن ${f}'\lt 0$ و ${f}''\lt 0$ باشد که تنها بازهٔ $(-2,0)$ این ویژگی را دارد. بنابراین حداکثر مقدار $b-a$ برابر 2 است.

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1403/03/17

عباس ابراهیمی علویجه

محتوای متنی دوره آموزشی، حسابان (2) دوازدهم دوره دوم متوسطه- نظری

مدرس: جابر عامری

مدت دوره: 220 صفحه (5 فایل)

با گنجینه سوال، آزمون دلخواهتو بساز

ترند شده

آزمون آمادگی امتحان نهایی حسابان (2) دوازدهم ریاضی + پاسخ | نمونه 4

2 صفحه

آزمون آمادگی امتحان نهایی حسابان (2) دوازدهم ریاضی + پاسخ | نمونه 4

کلاس دوازدهمی‌ها

ترند شده

آزمون آمادگی امتحان نهایی حسابان (2) دوازدهم ریاضی + پاسخ | نمونه 2

2 صفحه

آزمون آمادگی امتحان نهایی حسابان (2) دوازدهم ریاضی + پاسخ | نمونه 2

کلاس دوازدهمی‌ها

سوپراستار

بسته ویژه نمره بیست: 15 دوره امتحان نهایی درس حسابان (2) دوازدهم

72 صفحه

بسته ویژه نمره بیست: 15 دوره امتحان نهایی درس حسابان (2) دوازدهم

ويژه نامه نوبت اول و…

سوپراستار

4 سری نمونه سؤال آمادگی امتحان نهایی (نوبت دوم) حسابان (2) دوازدهم ریاضی

8 صفحه

4 سری نمونه سؤال آمادگی امتحان نهایی (نوبت دوم) حسابان (2) دوازدهم ریاضی

کلاس دوازدهمی‌ها

سئوالات موضوعی نهایی فصل دوم درس حسابان2 | مثلثات

11 صفحه

سئوالات موضوعی نهایی فصل دوم درس حسابان2 | مثلثات

جابر عامری

سوالات امتحان میان ترم حسابان دوازدهم دبیرستان شبانه روزی جلال آل احمد | فصل 1 و 2

4 صفحه

سوالات امتحان میان ترم حسابان دوازدهم دبیرستان شبانه روزی جلال آل احمد…

علی طاهری

رایـــــگان

سؤالات امتحان نهایی درس حسابان (2) دوازدهم رشته ریاضی | نوبت شهریور 99

5 صفحه

سؤالات امتحان نهایی درس حسابان (2) دوازدهم رشته ریاضی | نوبت شهریور 99

امتحان نهایی

آزمونک حسابان (2) دوازدهم دبیرستان دكتر طاهره صفار زاده | فصل 1: تابع

1 صفحه

آزمونک حسابان (2) دوازدهم دبیرستان دكتر طاهره صفار زاده | فصل 1: تابع

زهرا بازیار

نمونه سوال شبه نهایی حسابان 2 پایه دوازدهم خرداد 1403 استان خراسان رضوی

7 صفحه

نمونه سوال شبه نهایی حسابان 2 پایه دوازدهم خرداد 1403 استان خراسان رضوی

مهدی کلاهی

آزمون نوبت اول حسابان (2) دوازدهم دبیرستان امام صادق (ع) | دی 1397 + پاسخ

2 صفحه

آزمون نوبت اول حسابان (2) دوازدهم دبیرستان امام صادق (ع) | دی 1397 + پاسخ

علی احمدی

موارد بیشتر

موارد بیشتر

ارسال فایل

نمودار تابع |y=|log(x-1) چجوری رسم می‌شود؟

در مورد فرمول انبساط و انقباض عمودی

تابع دو به توان x در تمام دامنه خود اکیداً صعودی است. درست یا غلط

موارد بیشتر

ارسال پرسش

موارد بیشتر