درس 1: توابع چند جمله‌ای- توابع صعودی و نزولی
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
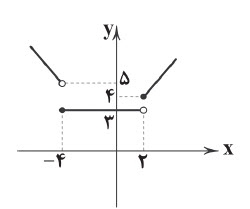
در مورد تابع $f(x)=\left\{ \begin{matrix}
-2x-3 \\
3 \\
3x-2 \\
\end{matrix} \right.\,\,\,\,\,\,\begin{matrix}
x\lt -4 \\
-4\le x\lt 2 \\
x\ge 2 \\
\end{matrix}$. کدام گزینه صحیح است؟
1 )
$f$ در فاصلهٔ $(-\infty ,0)$ نزولی اکید است.
$f$ در فاصلهٔ $(-4\,,\,+\infty )$ صعودی است.
3 )
$f$ در فاصلهٔ $(-\infty \,,\,-4)$ صعودی اکید است.
4 )
تابع $f$ هیچ بازهٔ ثابتی ندارد.
پاسخ تشریحی :
تحلیل ویدئویی تست
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...