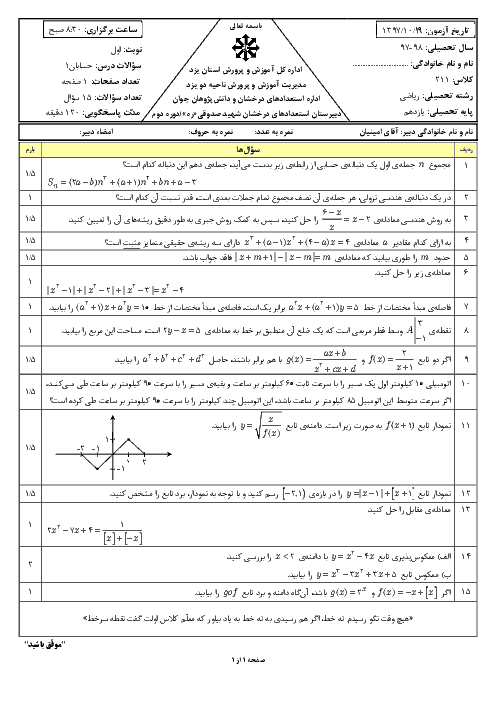
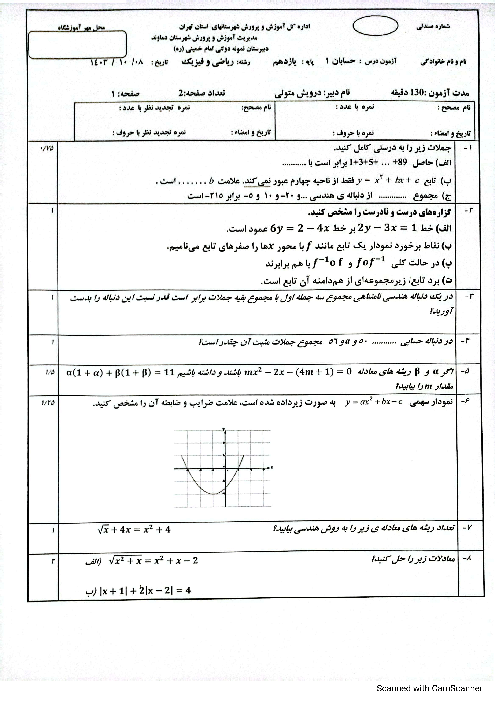
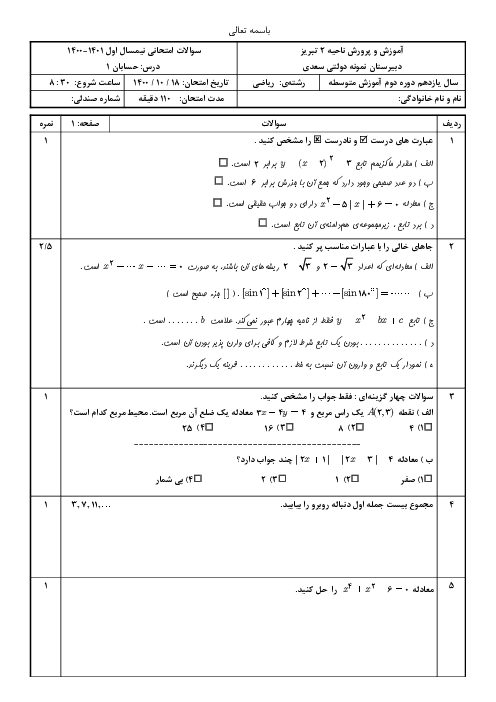
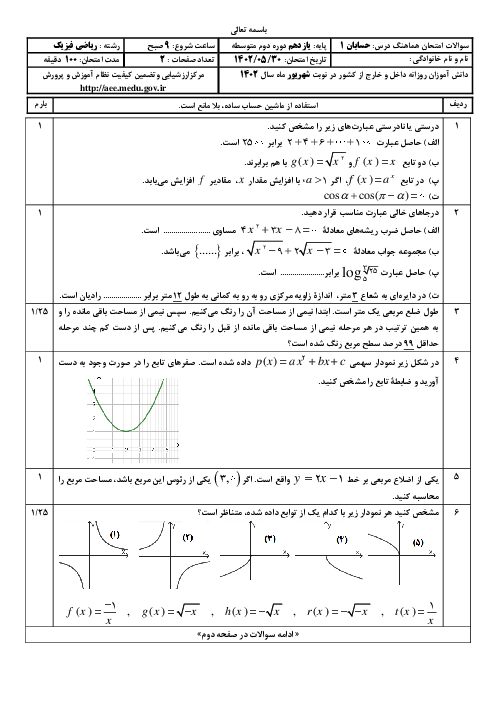
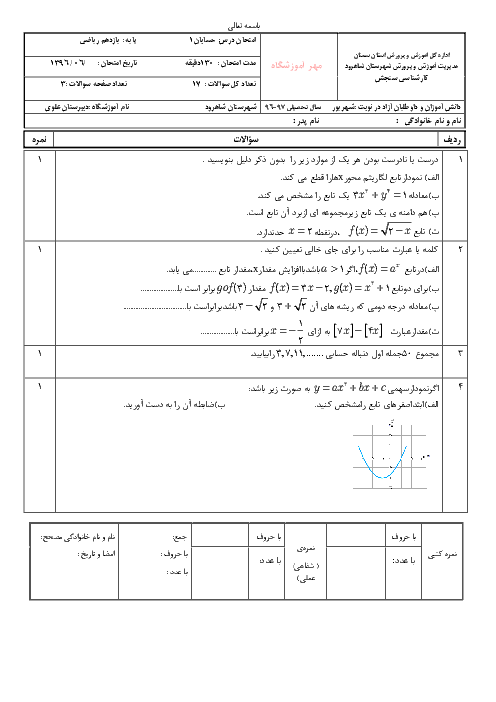
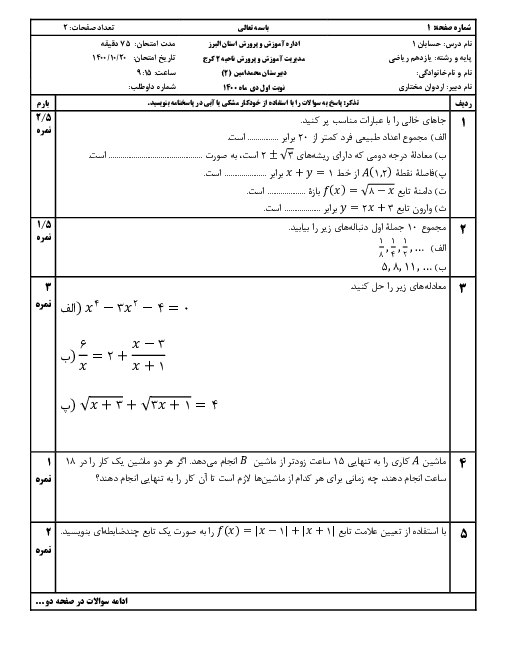
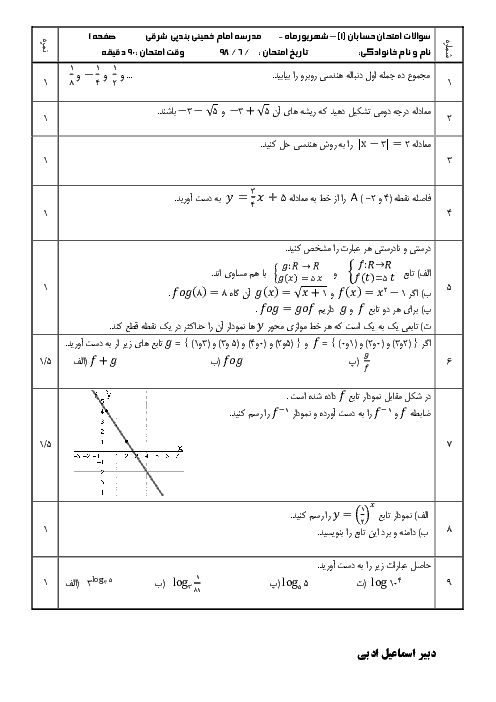
فرم معتبر نیست.
مقدار A را حساب کنید.
$ A = \frac{3}{{3 + Log_2^3}} + \frac{1}{{1 + 3Log_3^2}}$
پاسخ تشریحی :
نمایش پاسخ
$ A = \frac{3}{{3 + Log_2^3}} + \frac{1}{{Log_3^3 + 3Log_3^2}} = \frac{3}{{3Log_2^2 + Log_2^3}} + \frac{1}{{Log_3^3 + Log_3^8}}$
$= \frac{3}{{Log_2^8 + Log_2^3}} + \frac{1}{{Log_3^3 + Log_3^8}} = \frac{3}{{Log_2^{24}}} + \frac{1}{{Log_3^{24}}} = 3Log_{24}^2 + Log_{24}^3$
$ = Log_{24}^8 + Log_{24}^3 = Log_{24}^{24} = 1 $
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...