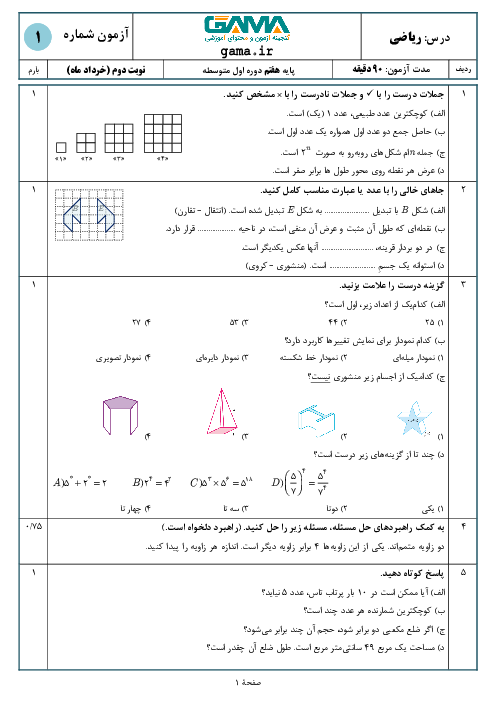
اگر $4\vec{AB} = 5\vec{BC}$ باشد و $ A = \begin{bmatrix} 7 \\ -3 \\ \end{bmatrix}$ و $ C = \begin{bmatrix} -2 \\ 6 \\ \end{bmatrix}$ باشند، مختصات نقطهی B کدام است؟
$ \begin{bmatrix} 2 \\ 2 \\ \end{bmatrix}$
2 )
$ \begin{bmatrix} 2 \\ 3 \\ \end{bmatrix}$
3 )
$ \begin{bmatrix} 3 \\ 5 \\ \end{bmatrix}$
4 )
$ \begin{bmatrix} 5 \\ 7 \\ \end{bmatrix}$
پاسخ تشریحی :
تحلیل ویدئویی تست
ریحانه احمدی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...